
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\ge\frac{5}{2}\)
\(pt\Leftrightarrow\sqrt{2x-5+2\sqrt{2x-5}+1}+\sqrt{2x-5+6\sqrt{2x-5}+9}=14\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2x-5}+1\right)^2}+\sqrt{\left(\sqrt{2x-5}+3\right)^2}=14\)
\(\Leftrightarrow\sqrt{2x-5}+1+\sqrt{2x-5}+3=14\)
\(\Leftrightarrow\sqrt{2x-5}=5\)
\(\Leftrightarrow2x-5=25\)
\(\Leftrightarrow x=15\left(TM\right)\)
Vậy phương trình đã cho có nghiệm duy nhất \(x=15\)

Mọi \(x_1;x_2\in\left(1;2\right)\)
G/s: \(x_1< x_2\)
Xét \(\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{\left(-x_1^2+\left(m-1\right)x_1+2\right)-\left(-x_2^2+\left(m-1\right)x_2+2\right)}{x_1-x_2}\)
\(=\frac{-\left(x_1^2-x_2^2\right)+\left(m-1\right)\left(x_1-x_2\right)}{\left(x_1-x_2\right)}\)
\(=-\left(x_1+x_2\right)+m-1\)
Để hàm số nghịch biến thì \(\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}< 0\Leftrightarrow m+1< x_1+x_2< 2+2\)=> \(m< 3\)



\(1,7-\left|x-2016\right|\)
Vì: \(-\left|x-2016\right|\le0\)
=> \(1,7-\left|x-2016\right|\le1,7\)
Dấu "=" xảy ra khi x-2016=0 <=> x=2016
Vậy GTLN của bt trên là 1,7 khi x=2016
bạn giải giúp mk câu này vơi: Tìm điểm (X0,Y0) thuộc đồ thị hàm số : y=mx-1/x-m với mọi giá trị của m
 Help me. Cần gấp😔😞😞😞
Help me. Cần gấp😔😞😞😞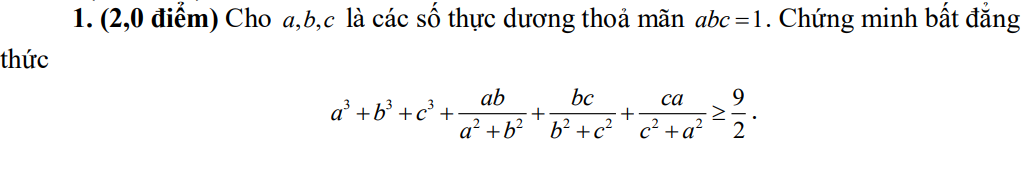 Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Giúp mình bài 6,8 với