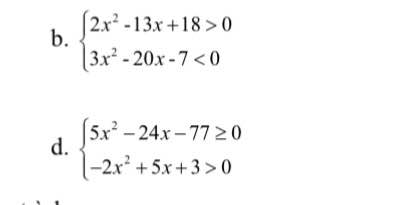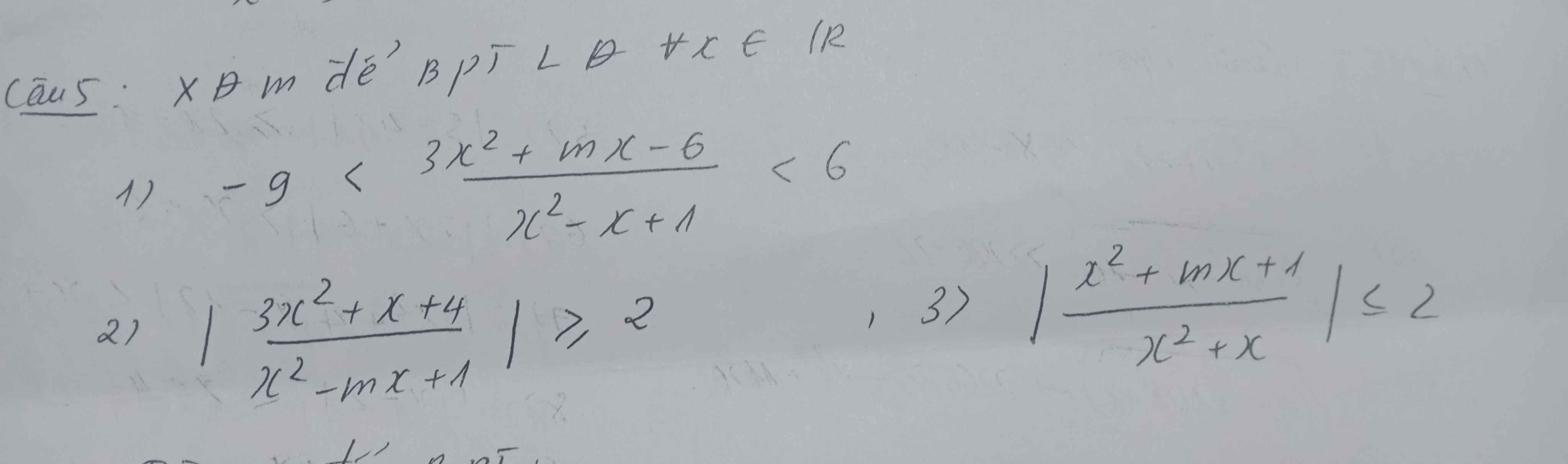K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
b.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 2\\x>\dfrac{9}{2}\end{matrix}\right.\\-\dfrac{1}{3}< x< 7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}< x< 2\\\dfrac{9}{2}< x< 7\end{matrix}\right.\)
Hay \(S=\left(-\dfrac{1}{3};2\right);\left(\dfrac{9}{2};7\right)\)
d.
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-\dfrac{11}{5}\\x\ge7\end{matrix}\right.\\-\dfrac{1}{2}< x< 3\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\) hay BPT vô nghiệm
26 tháng 6 2023
4:
a: =>4x^4-4x^2+x^2-1=0
=>(x^2-1)(4x^2+1)=0
=>x^2-1=0
=>x=1 hoặc x=-1
b: ĐKXĐ: x<>5; x<>2
PT =>\(\dfrac{x-2}{x-5}+3=\dfrac{6}{x-2}\)
=>\(x^2-4x+4+3\left(x^2-7x+10\right)=6x-30\)
=>4x^2-25x+34-6x+30=0
=>4x^2-31x+64=0
=>\(x\in\varnothing\)
c: =>x^2(2x^2+5)+2=0
=>x^2(2x^2+5)=-2(vôlý)
d: =>(2x-5)(x-2)=3x(x-1)
=>3x^2-3x=2x^2-4x-5x+10
=>x^2+6x-10=0
=>\(x=-3\pm\sqrt{19}\)
e: ĐKXĐ: x<>3; x<>-2
PT =>x^2-3x+5=x+2
=>x^2-4x+3=0
=>(x-3)(x-1)=0
=>x=1(nhận) hoặc x=3(loại)
f: ĐKXĐ: x<>2; x<>3
PT =>2x(x-3)-5(x-2)=5
=>2x^2-6x-5x+10-5=0
=>2x^2-11x+5=0
=>2x^2-10x-x+5=0
=>(x-5)(2x-1)=0
=>x=1/2 hoặc x=5
15 tháng 6 2023
5:
(d) vuông góc 2x-y-2018=0
=>(d): x+2y+c=0
(C): x^2+4x+4+y^2-6y+9-25=0
=>(x+2)^2+(y-3)^2=25
=>R=5; I(-2;3)
Theo đề, ta có: d(I;(d))=5
=>\(\dfrac{\left|1\cdot\left(-2\right)+2\cdot3+c\right|}{\sqrt{5}}=5\)
=>|c+4|=5căn 5
=>c=5căn5-4 hoặc c=-5căn 5-4
QN
0
22 tháng 1 2022
Bài 6:
b: x+3y-6=0
=>x+3y=6
=>3y=6-x
=>y=-1/3x+2
Vì (d) vuông góc với y=-1/3x+2 nên -1/3a=-1
=>a=3
Vậy: (d): y=3x+b
Thay x=2 và y=5 vào (d), ta được:
b+6=5
hay b=-1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 11 2021
ĐKXĐ: \(-1\le x\le3\)
Đặt \(\sqrt{x+1}+\sqrt{3-x}=t\ge\sqrt{x+1+3-x}=2\)
\(\Rightarrow4+2\sqrt{-x^2+2x+3}=t^2\)
\(\Rightarrow\sqrt{-x^2+2x+3}=\dfrac{t^2-4}{2}\) (1)
Phương trình trở thành:
\(t-\dfrac{t^2-4}{2}=2\)
\(\Leftrightarrow2t-t^2=0\Rightarrow\left[{}\begin{matrix}t=0\left(loại\right)\\t=2\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\sqrt{-x^2+2x+3}=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)