
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì: BC=DC
mà M,N là trung điểm của BC,DC
=> BM=MC=DN=NC=1cm
\(S_{AMN}=S_{ABCD}-S_{ADN}-S_{ABM}-S_{NMC}\)
\(=AB\cdot AB-\frac{1}{2}\cdot AD\cdot DN-\frac{1}{2}AB\cdot BM-\frac{1}{2}NC\cdot MC\)
\(=2\cdot2-\frac{1}{2}\cdot2\cdot1-\frac{1}{2}\cdot2\cdot1-\frac{1}{2}\cdot1\cdot1\)
\(=4-1-1-\frac{1}{2}=1,5\)

Ta có : \(\frac{\sqrt{4m^2-8mn+4n^2}}{3n-3m}=\frac{\sqrt{4\left(m^2-4mn+n^2\right)}}{3\left(n-m\right)}\)
\(=\frac{2\sqrt{\left(m-n\right)^2}}{3\left(n-m\right)}=\frac{2\left|m-n\right|}{3\left(n-m\right)}=\frac{2\left(n-m\right)}{3\left(n-m\right)}=\frac{2}{3}\)(vì m<n)
\(\frac{\sqrt{4m^2-8mn+4n^2}}{3n-3m}=\frac{\sqrt{4\left(m^2-4mn+m^2\right)}}{3\left(n-m\right)}=\frac{\sqrt{4\left(m-n\right)^2}}{3\left(n-m\right)}=\frac{2\left(m-n\right)}{3\left(n-m\right)}=-\frac{2}{3}\)


1)\(\sqrt{x-2+2\sqrt{x-3}}\)=\(\sqrt{(x-3)+2\sqrt{x-3}+1}=\sqrt{(\sqrt{x-3}+1)^2}=\sqrt{x-3}+1 \)
2)\(\sqrt{x-1-2\sqrt{x-2}}=\sqrt{x-2-2\sqrt{x-2}+1}=\sqrt{(\sqrt{x-2}-1)^2}=\sqrt{x-2}-1\)

b: \(=x-4\sqrt{x}+3\sqrt{x}-12=\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)\)

Áp dụng định lí Pytago vào tam giác vuông ADH :
\(DH^2=AD^2-AH^2=2^2-3=1\Rightarrow DH=1\) (cm)
Theo hệ thức trong tam giác : \(AD^2=HD.BD\Rightarrow BD=\frac{AD^2}{DH}=\frac{2^2}{1}=4\) (cm)


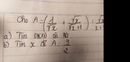
 help me
help me



 help me
help me vs
vs


 help me pls
help me pls



bổ sung đề : mình ko biết đúng ko nhưng ko phải đăng lại giải lại :))
a, \(A=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : \(x>0\)
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
b, Với \(A=\frac{9}{2}\Rightarrow\frac{x+\sqrt{x}+1}{\sqrt{x}}=\frac{9}{2}\)
\(\Rightarrow2x+2\sqrt{x}+2=9\sqrt{x}\Leftrightarrow2x-7\sqrt{x}+2=0\)
\(\Leftrightarrow x=\sqrt{\frac{7\pm\sqrt{33}}{4}}\) kết hợp với đk vậy : \(x=\sqrt{\frac{7+\sqrt{33}}{4}}\)
Đáp án :
- Bình phương lê nha bn