Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: \(=\left(4+\sqrt{3}\right)\cdot\sqrt{\left(4-\sqrt{3}\right)^2}\)
=(4+căn 3)(4-căn 3)
=16-3=13
d: \(=\sqrt{6+2\sqrt{5-2\sqrt{3}-1}}\)
\(=\sqrt{6+2\cdot\sqrt{4-2\sqrt{3}}}\)
\(=\sqrt{6+2\cdot\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{23-8\sqrt{5}}\)
\(=\left|1-\sqrt{5}\right|+\sqrt{23-2\sqrt{60}}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}\right)^2-2.\sqrt{20}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}-\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{20}-\sqrt{3}=\sqrt{5}+2\sqrt{5}-1-\sqrt{3}\)
\(=3\sqrt{5}-1-\sqrt{3}\)

Đề bài không rõ ràng, em liên hệ người ra đề xem vẽ đồ thị đường thẳng nào? Vì đường thẳng đề cho có a chưa biết


a: Xét tứ giác OEAF có
\(\widehat{OEA}+\widehat{OFA}=180^0\)
Do đó: OEAF là tứ giác nội tiếp

a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)

a: Xét tứ giác AMHK có
\(\widehat{MAK}=\widehat{AKH}=\widehat{AMH}=90^0\)
Do đó: AMHK là hình chữ nhật
Suy ra: AH=KM(1)
Xét ΔAHC vuông tại H có
\(AM\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=MK^2\)

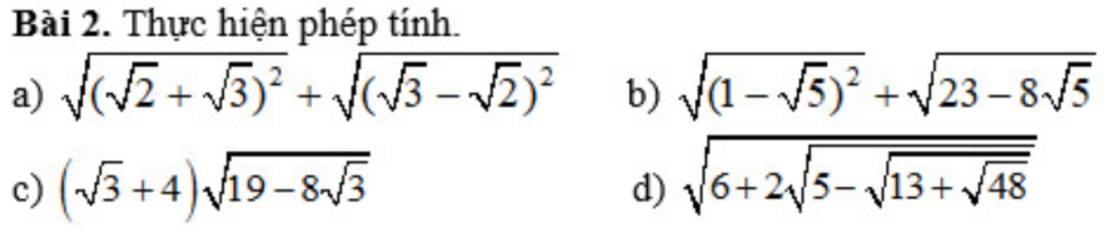 câu b, c, d thôi ạ!
câu b, c, d thôi ạ!

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 
 giải câu d thôi ạ
giải câu d thôi ạ


Câu c tính gì vậy bạn?
tính BC nhé !