Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a = 2002 x 2002 = ( 2000 + 2 ) x 2002
= 2000 x 2002 + 2 x 2002
b = 2000 x 2004 = 2000 x ( 2002 + 2 )
= 2000x 2002 + 2 x 2000
ta thấy 2000 x 2002 + 2 x 2002 > 2000 x 2002 + 2 x 2000 nên a > b
a=2002x2002
a=(2000+2)x2002
a=2000x2002+2x2002
a=2000x2002+2x(2000+2)
a=2000x2002+2x2000+4
a=2000x(2002+2)+4
a=2000x2004+4
a=b+4
Vậy a lớn hơn b và lớn hơn 4 đơn vị.

Lời giải:
Gọi ƯCLN(a,b) = d thì $a=dx, b=dy$ với $x,y$ là 2 số tự nhiên nguyên tố cùng nhau.
BCNN(a,b) = dxy
Theo bài ra ta có: $dxy+d=15$
$d(xy+1)=15$
$\Rightarrow 15\vdots d$ nên $d\in\left\{1;3;5;15\right\}$
Nếu $d=1$ thì $xy+1=15\Rightarrow xy=14$.
Do $x,y$ nguyên tố cùng nhau nên $(x,y)=(1,14), (14,1), (2,7), (7,2)$
$\Rightarrow (a,b)=(1,14), (14,1), (2,7), (7,2)$
Nếu $d=3$ thì $xy=4$. Do $x,y$ nguyên tố cùng nhau nên $(x,y)=(1,4), (4,1)$
$\Rightarrow (a,b)=(3,12), (12,3)$
Nếu $d=5$ thì $xy=2$. Do $x,y$ nguyên tố cùng nhau nên $(x,y)=(2,1), (1,2)$
$\Rightarrow (a,b)=(10,5), (5,10)$
Nếu $d=15$ thì $xy=0$ (vô lý, loại)

Ta có : \(A=\frac{2010^{2011+1}}{2010^{2010+1}}=\frac{2010^{2012}}{2010^{2011}}\)
Lại có \(B=\frac{2010^{2012+1}}{2010^{2011}}=\frac{2010^{2013}}{2010^{2011}}\)
Suy ra \(\frac{2010^{2012}}{2010^{2011}}< \frac{2010^{2013}}{2010^{2011}}\)
=> A < B
Chúc bạn thi tốt
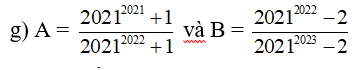
bn đưa về cùng cơ số hoặc số mũ là giải đc đó ^^
Các bạn làm giúp mk với mk đang cần gấp