K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 4 2018
Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
LH
22 tháng 4 2017
Ví dụ: phương trình (1) x - 1 = 3 có tập nghiệm S1 = {4}.
Nhân hai vế của phương trình (1) với x, ta được phương trình:
(x - 1)x = 3x (2)
⇔ (x - 1)x - 3x = 0
⇔ x(x - 4) = 0
Phương trình (2) có tập nghiệm là S2 = {0, 4}.
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
3. Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số).
NH
1
6 tháng 3 2016
Nhâ hai vế của một phương tình với cùng một biểu thức chứa ẩn thì có thể không được phương trình tương đương. VD:\(0=\frac{x^2+4x}{x}\)
PT
1
CM
22 tháng 7 2017
Bất phương trình bậc nhất một ẩn có dạng: ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a, b là hai số đã cho, a ≠ 0.
Ví dụ: 2x + 4 < 0 (hoặc 2x + 4 > 0, 2x + 4 ≤ 0, 2x + 4 ≥ 0)
SG
3
LS
22 tháng 4 2017
Bất phương trình bậc nhất một ẩn có dạng: ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a, b là hai số đã cho, a ≠ 0.
Ví dụ: 2x + 4 < 0 (hoặc 2x + 4 > 0, 2x + 4 ≤ 0, 2x + 4 ≥ 0)
KV
10 tháng 5 2023
a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c)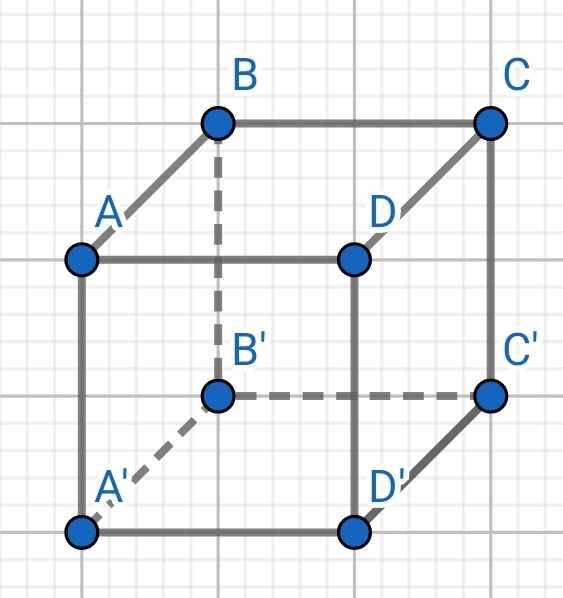 
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
10 tháng 5 2023
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3
Phương trình với ẩn u: 2u – 11 = 3(u+1)