Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

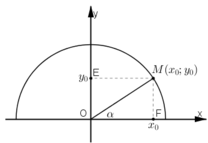
Gọi E, F lần lượt là hình chiếu của M trên Oy, Ox.
Khi đó xét ΔMOF vuông tại F thì :
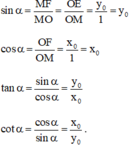

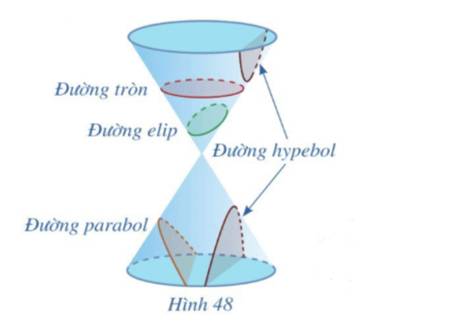
Đường conic gồm 3 loại đường đó là: elip, hypebol, parabol

Khi tới vị trị M(3;4), vật bị văng khỏi quỹ đạo tròn và ngay sau đó bay theo hướng tiếp tuyến d của đường tròn tại điểm M. Do đó, d đi qua điểm M và nhận vecto \(\overrightarrow {OM} = \left( {3;4} \right)\) làm vecto pháp tuyến. Vậy phương trình của d là: \(3\left( {x - 3} \right) + 4\left( {y - 4} \right) = 0 \Leftrightarrow 3x + 4y - 25 = 0\).

Điểm \(M\left( {x;y} \right)\) thuộc đường tròn \(\left( C \right)\) tâm \(I\left( {a;b} \right)\), bán kính \(R\) khi và chỉ khi \(MI = R \Leftrightarrow \sqrt {{{(x - a)}^2} + {{(y - b)}^2}} = R\) hay \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

a)
Bước 1:
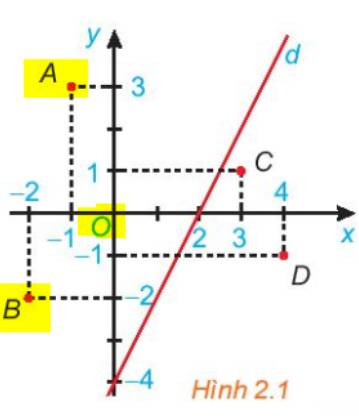
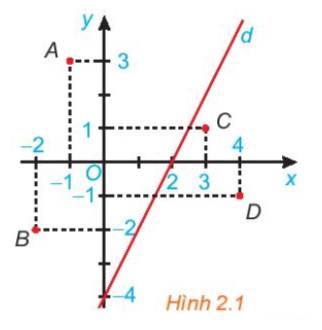
Quan sát hình trên, các điểm A, O, B là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên trái) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Bước 2:
+) Thay tọa độ của điểm O(0;0) vào biểu thức 2x-y ta được: 2.0-0=0.
Như vậy giá trị của biểu thức 2x-y tại O là 0 và 0<4.
+) Thay tọa độ của điểm A(-1;3) vào biểu thức 2x-y ta được: 2.(-1)-3=-5.
Như vậy giá trị của biểu thức 2x-y tại A là -5 và -5<4
+) Thay tọa độ của điểm B(-2;-2) vào biểu thức 2x-y ta được: 2.(-2)-(-2)=-2.
Như vậy giá trị của biểu thức 2x-y tại B là -2 và -2<4.
b)
Bước 1:
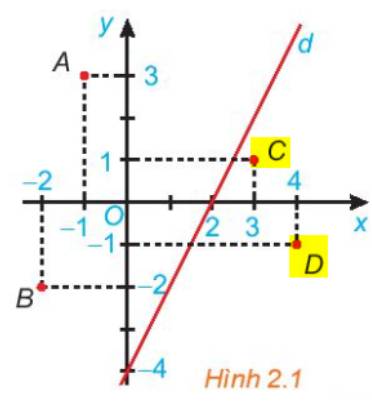
Quan sát hình trên, các điểm C, D là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên phải) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Bước 2:
+) Thay tọa độ của điểm C(3;1) vào biểu thức 2x-y ta được: 2.3-1=5.
Như vậy giá trị của biểu thức 2x-y tại C là 5 và 5>4.
+) Thay tọa độ của điểm D(4;-1) vào biểu thức 2x-y ta được: 2.4-(-1)=9.
Như vậy giá trị của biểu thức 2x-y tại D là 9 và 9>4
Chú ý
Khi thay tọa độ các điểm vào biểu thức 2x-y, nếu y là một giá trị âm thì cần đưa nguyên dấu vào trong biểu thức.

a:góc ABD=góc DCA
góc ABD=góc FAD(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD)
góc FAD=góc CAD
=>góc ABD=góc CBD
=>BD là phân giác của góc ABE
mà góc ADB=90 độ
nên BD là đường cao
=>ΔBAE cân tại B
b: Xét ΔEAB có
AC,BD là các đường cao
AC cắt BD tại K
Do đó: K là trực tâm
=>EK vuông góc với BA
c: Xét ΔAKF có AD vừa là đường cao, vừa là phân giác
nên ΔAKF cân tại A
=>góc AKF=góc AFK=góc KFE
=>AK//FE
Xét tứ giác AKEF có
AK//FE
AF//KE
KE=KA
Do đó: AKEF là hình thoi

Bóng của đường tròn trên mặt phẳng không phải là đường tròn.