QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
Hệ số góc của đường thẳng \({d_1}:y = 3x\) là \(a = 3\);
Hệ số góc của đường thẳng \({d_2}:y = - 7x + 9\) là \(a = - 7\);
Hệ số góc của đường thẳng \({d_3}:y = 3x - 0,8\) là \(a = 3\);
Hệ số góc của đường thẳng \({d_4}:y = - 7x - 1\) là \(a = - 7\);
Hệ số góc của đường thẳng \({d_5}:y = \sqrt 2 x + 10\) là \(a = \sqrt 2 \);
Hệ số góc của đường thẳng \({d_6}:y = \sqrt 2 x + \sqrt {10} \) là \(a = \sqrt 2 \);
- Các cặp đường thẳng song song là:
\({d_1}:y = 3x\) và \({d_3}:y = 3x - 0,8\) vì đều có hệ số góc \(a = 3\) và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
\({d_2}:y = - 7x + 9\) và \({d_4}:y = - 7x - 1\) vì đều có hệ số góc \(a = - 7\)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
\({d_5}:y = \sqrt 2 x + 10\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì đều có hệ số góc \(a = \sqrt 2 \)và chúng phân biệt với nhau do chúng cắt \(Oy\) tại hai điểm phân biệt.
- Ba cặp đường thẳng cắt nhau là:
\({d_1}:y = 3x\) và \({d_4}:y = - 7x - 1\) vì có hệ số góc khác nhau \(\left( {3 \ne - 7} \right)\).
\({d_2}:y = - 7x + 9\) và \({d_6}:y = \sqrt 2 x + \sqrt {10} \) vì có hệ số góc khác nhau \(\left( { - 7 \ne \sqrt 2 } \right)\).
\({d_3}:y = 3x - 0,8\) và \({d_5}:y = \sqrt 2 x + 10\) vì có hệ số góc khác nhau \(\left( {3 \ne \sqrt 2 } \right)\).
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
Hệ số góc của đường thẳng \({d_1}:y = 0,2x\) là \(a = 0,2\);
Hệ số góc của đường thẳng \({d_2}:y = - 2x + 4\) là \(a = - 2\);
Hệ số góc của đường thẳng \({d_3}:y = 0,2x - 0,8\) là \(a = 0,2\);
Hệ số góc của đường thẳng \({d_4}:y = - 2x - 5\) là \(a = - 2\);
Hệ số góc của đường thẳng \({d_5}:y = \sqrt 3 x + 3\) là \(a = \sqrt 3 \);
Hệ số góc của đường thẳng \({d_6}:y = \sqrt 3 x - \sqrt 5 \) là \(a = \sqrt 3 \);
- Các cặp đường thẳng song song là:
\({d_1}:y = 0,2x\) và \({d_3}:y = 0,2x - 0,8\) vì đều có hệ số góc \(a = 0,2\) và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
\({d_2}:y = - 2x + 4\) và \({d_4}:y = - 2x - 5\) vì đều có hệ số góc \(a = - 2\)và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
\({d_5}:y = \sqrt 3 x + 3\) và \({d_6}:y = \sqrt 3 x - \sqrt 5 \) vì đều có hệ số góc \(a = \sqrt 3 \) và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
- Ba cặp đường thẳng cắt nhau là:
\({d_1}:y = 0,2x\) và \({d_2}:y = - 2x + 4\) vì có hệ số góc khác nhau \(\left( {0,2 \ne - 2} \right)\).
\({d_3}:y = 0,2x - 0,8\) và \({d_4}:y = - 2x - 5\)vì có hệ số góc khác nhau \(\left( {0,2 \ne - 2} \right)\).
\({d_5}:y = \sqrt 3 x + 3\) và \({d_4}:y = - 2x - 5\) vì có hệ số góc khác nhau \(\left( {\sqrt 3 \ne - 2} \right)\).
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
12 tháng 9 2023
Ba cặp đường thẳng cắt nhau: d1 và d2, d2 và d3, d4 và d5
Các cặp đường thẳng song song: d1 và d3, d2 và d4, d5 và d6
KV
4 tháng 12 2023
(d1): 2x + y - 3 = 0
y = -2x + 2
(d2): y = 5 - 2x
y = -2x + 5
(d3): 2y = x + 4
y = x/2 + 2
(d4): x + y - 1 = 0
y = -x + 1
*) Cặp đường thẳng song song:
(d1) và (d2)
*) Các cặp đường thẳng cắt nhau:
(d1) và (d3); (d1) và (d4); (d2) và (d3); (d2) và (d4); (d3) và (d4)
CM
20 tháng 2 2018
Định lí:
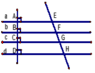
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.
16 tháng 5 2022
a) Các đường thẳng song song với nhau:
- Hai đường thẳng mép thước kẻ đối diện nhau.
- Hai đường thẳng mép bàn đối diện nhau.
b) Các đường thẳng cắt nhau:
- Các đường thẳng góc tường và chân tường là hai đường thẳng cắt nhau.
- Hai thanh chắn khung cửa sổ cắt nhau.
c) Các mặt phẳng song song với nhau
- Mặt sàn nhà và mặt trần nhà là hai mặt phẳng song song
d) Các đường thẳng vuông góc với nhau
- Hai cạnh góc vuông của thước eke
e) Các đường thẳng vuông góc với các mặt phẳng:
- Đường góc tường vuông góc với mặt sàn hoặc với trần nhà.
f) Các mặt phẳng vuông góc với nhau:
- Tường nhà vuông góc với nền nhà.
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
Các cặp song song là: y = −x + 1 và y = −x; y = −2x + 1 và y = −2x + 2
Các cặp đường thẳng cắt nhau là: y = −x + 1 và y = −2x + 2; y = −x và y = −2x + 1; y = −x + 1 và y = −2x + 1; y = −x và y = −2x + 2
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
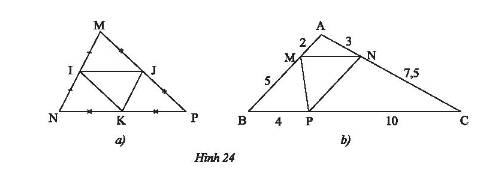
a) Theo hình vẽ ta có:
\(I\) là trung điểm của \(MN\) nên \(IM = IN = \frac{1}{2}MN\);
\(J\) là trung điểm của \(MP\) nên \(JM = JP = \frac{1}{2}MP\);
\(K\) là trung điểm của \(NP\) nên \(KN = KP = \frac{1}{2}NP\).
Xét tam giác \(MNP\) có:
\(\frac{{IM}}{{MN}} = \frac{1}{2};\frac{{MJ}}{{PJ}} = \frac{1}{2} \Rightarrow \frac{{IM}}{{MN}} = \frac{{MJ}}{{PJ}} \Rightarrow IJ//NP\) (Định lí Thales đảo);
\(\frac{{PJ}}{{PM}} = \frac{1}{2};\frac{{PK}}{{PN}} = \frac{1}{2} \Rightarrow \frac{{PJ}}{{PM}} = \frac{{PK}}{{PN}} \Rightarrow JK//MN\) (Định lí Thales đảo);
\(\frac{{NK}}{{NP}} = \frac{1}{2};\frac{{IN}}{{MN}} = \frac{1}{2} \Rightarrow \frac{{NK}}{{NP}} = \frac{{IN}}{{MN}} \Rightarrow IK//MN\) (Định lí Thales đảo).
b) Xét tam giác \(ABC\) có:
\(\frac{{AN}}{{NC}} = \frac{3}{{7,5}} = \frac{2}{5};\frac{{AM}}{{BM}} = \frac{2}{5} \Rightarrow \frac{{AN}}{{NC}} = \frac{{AM}}{{BM}} \Rightarrow MN//BC\)(Định lí Thales đảo);
\(\frac{{CN}}{{AN}} = \frac{{7,5}}{3} = \frac{5}{2};\frac{{CP}}{{PB}} = \frac{{10}}{4} = \frac{5}{2} \Rightarrow \frac{{CN}}{{AN}} = \frac{{CP}}{{BP}} \Rightarrow NP//AB\)(Định lí Thales đảo);
\(\frac{{BM}}{{AM}} = \frac{5}{2};\frac{{PB}}{{CP}} = \frac{4}{{10}} = \frac{2}{5} \Rightarrow \frac{{BM}}{{AM}} \ne \frac{{BP}}{{CP}} \Rightarrow NP\) không song song với \(AB\)(Định lí Thales đảo).
CM
24 tháng 8 2019
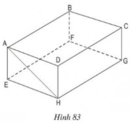
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
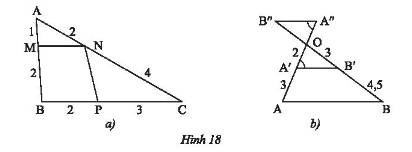
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).