
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


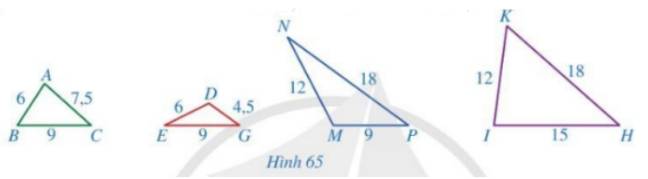
Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)

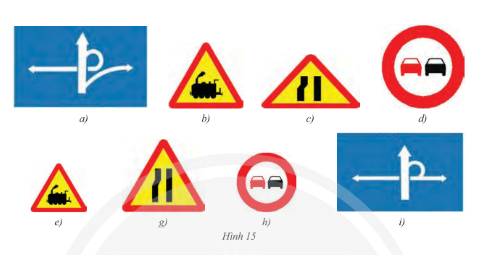
Các cặp hình đồng dạng là:
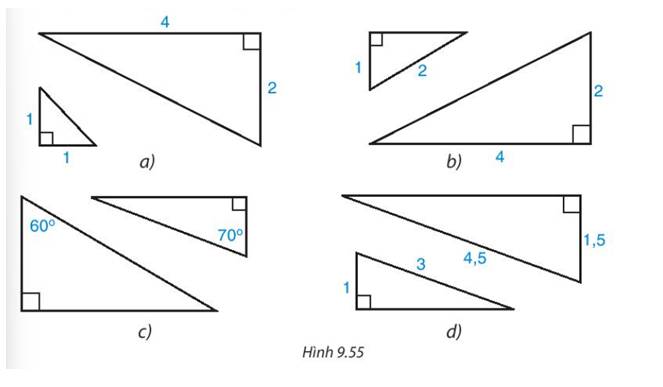
- Hình a và hình i đồng dạng với nhau;
- Hình b và hình e đồng dạng với nhau;
- Hình c và hình g đồng dạng với nhau;
- Hình d và hình h đồng dạng với nhau.

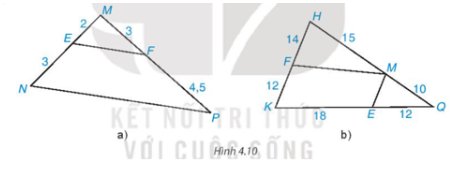
• Hình 4.10a)
Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)
Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.
* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)
Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.

Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)

a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).

\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow B'C' = \frac{{BC.A'B'}}{{AB}}\).

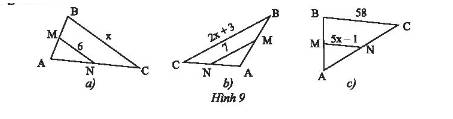
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6
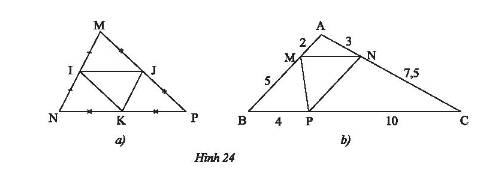



a) Theo hình vẽ ta có:
\(I\) là trung điểm của \(MN\) nên \(IM = IN = \frac{1}{2}MN\);
\(J\) là trung điểm của \(MP\) nên \(JM = JP = \frac{1}{2}MP\);
\(K\) là trung điểm của \(NP\) nên \(KN = KP = \frac{1}{2}NP\).
Xét tam giác \(MNP\) có:
\(\frac{{IM}}{{MN}} = \frac{1}{2};\frac{{MJ}}{{PJ}} = \frac{1}{2} \Rightarrow \frac{{IM}}{{MN}} = \frac{{MJ}}{{PJ}} \Rightarrow IJ//NP\) (Định lí Thales đảo);
\(\frac{{PJ}}{{PM}} = \frac{1}{2};\frac{{PK}}{{PN}} = \frac{1}{2} \Rightarrow \frac{{PJ}}{{PM}} = \frac{{PK}}{{PN}} \Rightarrow JK//MN\) (Định lí Thales đảo);
\(\frac{{NK}}{{NP}} = \frac{1}{2};\frac{{IN}}{{MN}} = \frac{1}{2} \Rightarrow \frac{{NK}}{{NP}} = \frac{{IN}}{{MN}} \Rightarrow IK//MN\) (Định lí Thales đảo).
b) Xét tam giác \(ABC\) có:
\(\frac{{AN}}{{NC}} = \frac{3}{{7,5}} = \frac{2}{5};\frac{{AM}}{{BM}} = \frac{2}{5} \Rightarrow \frac{{AN}}{{NC}} = \frac{{AM}}{{BM}} \Rightarrow MN//BC\)(Định lí Thales đảo);
\(\frac{{CN}}{{AN}} = \frac{{7,5}}{3} = \frac{5}{2};\frac{{CP}}{{PB}} = \frac{{10}}{4} = \frac{5}{2} \Rightarrow \frac{{CN}}{{AN}} = \frac{{CP}}{{BP}} \Rightarrow NP//AB\)(Định lí Thales đảo);
\(\frac{{BM}}{{AM}} = \frac{5}{2};\frac{{PB}}{{CP}} = \frac{4}{{10}} = \frac{2}{5} \Rightarrow \frac{{BM}}{{AM}} \ne \frac{{BP}}{{CP}} \Rightarrow NP\) không song song với \(AB\)(Định lí Thales đảo).