Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

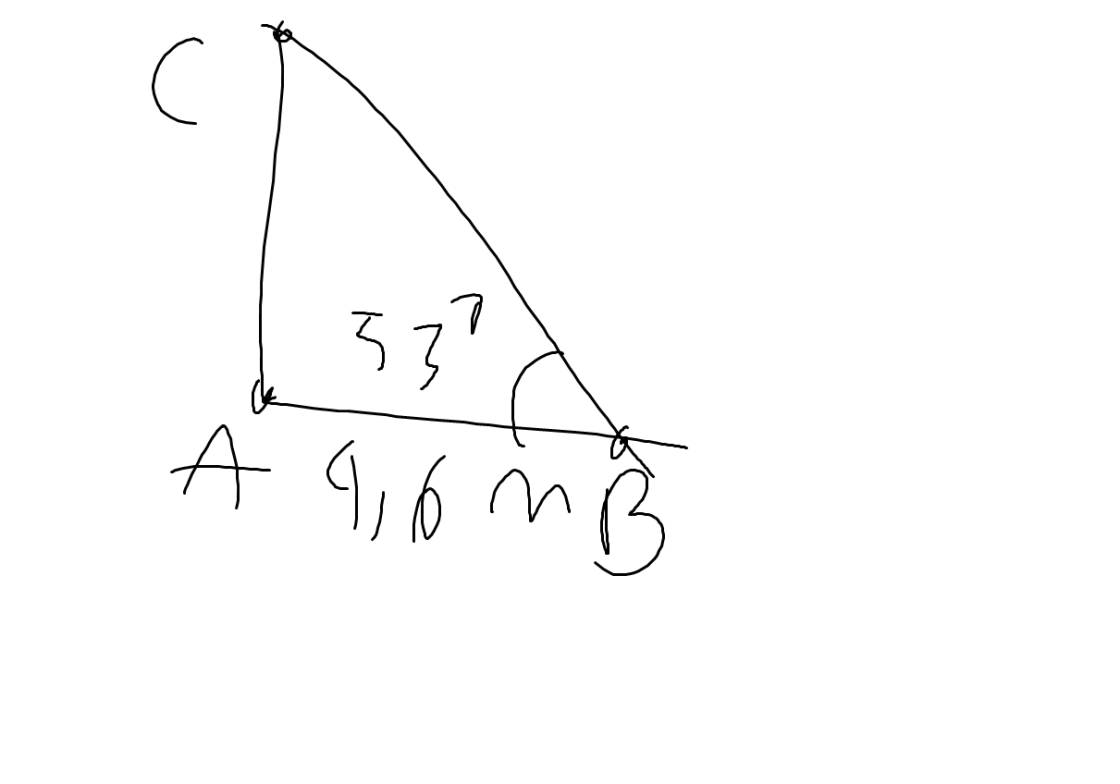
Gọi chiều cao của cây nêu là AC, bóng của cây nêu trên mặt đất là AB
Theo đề, ta có: AB\(\perp\)AC tại A, AB=4,6m; \(\widehat{B}=53^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{4,6}=tan53\)
=>\(AC\simeq6\left(m\right)\)
vậy: Chiều cao của cây nêu khoảng 6m

Chiều cao của cái cây đó là:
4,5*tan55\(\simeq6,43\left(m\right)\)

Gọi chân cột đèn là điểm A, đỉnh cột đèn là điểm B và bóng của đỉnh cột trên mặt đất là C
Ta có tam giác ABC vuông tại A với \(AC=7,5\left(m\right)\) và \(\widehat{BCA}=42^0\)
Trong tam giác vuông ABC:
\(AB=AC.tan\widehat{BAC}=7,5.tan42^0\approx6,8\left(m\right)\)

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)

Gọi tam giác tại bởi phần thân cây bị gãy với phần cây còn lại và mặt đất là △ ABC vuông tại A. Ta có
cos 20 = 7.5 / cạnh huyền
⇒ cạnh huyền = \(\dfrac{7,5}{cos20}\)\(\approx\) 8 ( m )
Áp dụng định lý Py-ta-go ta có:
phần bị gãy của cây cau là : \(\sqrt{8^2-7,5^2}\) = 2.78 ( m )
⇒ Chiều cao cây cau lúc đầu là : 8 + 2.78 =10.78 ( m )