PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
12 tháng 12 2018
Đáp án C
Phương pháp:
Sử dụng phương pháp tìm GTNN, GTLN của hàm số.
Cách giải:
CM
30 tháng 11 2019
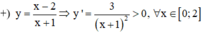
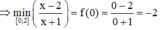
Chọn A
Tập xác định D = [0;4]
Ta có 
Vì 
=> Giá trị lớn nhất của hàm số là y = 2 khi x = 2
Mặt khác 
=> Giá trị nhỏ nhất của hàm số là y = 0 khi x = 4 hoặc
Vậy hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
CM
20 tháng 11 2019
Chọn B
Nếu m = 1 thì y = 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu m
≠
1 thì hàm số đã cho liên tục trên [1;2] và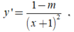 
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn [1;2]
Do vậy 
CM
19 tháng 11 2019
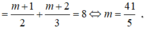
Chọn D.
Xét hàm số 
hàm số liên tục trên R
Có 
đồng biến trên [2;4]
Nên 
Do đó 
Ta có 
Dấu bằng xảy ra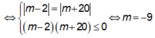 
Vậy 
CM
29 tháng 7 2018
Đáp án: A.
Tập xác định: D = R \{3}
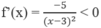∀x ∈ D.
Do đó f(x) nghịch biến trên (- ∞ ; 3) và (3; + ∞ ).
Ta thấy [0;2] ⊂ (- ∞ ;3). Vì vậy
max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.
PT
1
CM
30 tháng 11 2017
Đáp án: D.
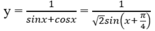
Trên khoảng (0; π/2), sin(x + π/4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π/4
Suy ra giá trị nhỏ nhất của hàm số là min y = y(π/4) = 2 /2.
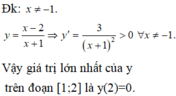
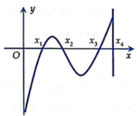
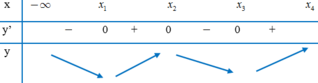
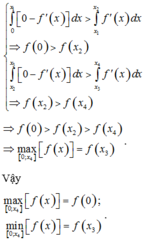
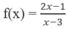
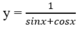
Đáp án D