Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số thứ nhất là x
=> Số thứ 2 là 20/9 x
Thương của số thứ nhất và 3 là 1/3 x
Thương của số thứ 2 và 4 là 5/9x
Theo bài ra ta có PT:
1/3 x + 4= 5/9 x
<=> −2/9−29 x = -4
<=> x = 18
Số thứ 2 là:
18. 20/9 = 40
Vậy số thứ 1 là 18, số thứ 2 là 40
#Châu's ngốc
Một chiếc xe tải đi từ điểm A đến điểm B, quãng đường dài 172 km. Sau khi xe tải xuất phát được 1 giờ, một chiếc xe khách bắt đầu đi từ B về A và gặp xe tải sau khi đã đi được 1 giờ 36 phút. Tính vận tốc mỗi xe biết rằng mỗi giờ xe khách đi nhanh hơn xe tải 13 km.

Gọi x là mẫu số, 4/5x là tử số (x,y thuộc N*)
Theo đề bài:Nếu lấy số thứ nhất chia cho 4 , số thứ hai chia cho 3 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị nên:
\(\frac{x}{3}-\frac{\frac{4}{5}x}{4}=2\)
=> x= 15
vậy số cần tìm là 12 và 15

Gọi a (a ∈ N *) là số thứ nhất. Ta có số thứ hai là 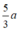
Thương phép chia số thứ nhất cho 9 là a/9
Thương phép chia số thứ hai cho 6 là: 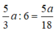
Thương thứ nhất bé hơn thương thứ hai là ba đơn vị nên ta có phương trình:
5a/18 - a/9 = 3
⇔ 5a/18 - 2a/18 = 54/18
⇔ 5a – 2a = 54
⇔ 3a = 54 ⇔ a = 18 (thỏa mãn)
Vậy số thứ nhất là 18, số thứ hai là 5/3.18 = 30.

Bài làm
Gọi số thứ nhất là 4.a = 4a
Số thứ hai là 7.a = 7a
Vì là số nguyên dương nên a>0
Ta có phương trình: 4a/4 - 7a/9 = 2
Hay a - 7a/9 = 2
<=> 36a/36 - 28a/36 = 2
<=> (36a-28a)/2 = 2
<=> 4a/2 = 2
<=> 2a = 2
<=> a = 1
Mà a > 0
=> a = 1 thoả mãn
Ta có: số thứ nhất là: 4a = 4 .1 = 4
Số thứ hai là: 7a = 7 .1 = 7
V

+) Gọi số thứ nhất (ban đầu) là x. (x: nguyên, dương)
Khi đó số thứ hai (ban đầu) là \(\dfrac{3}{5}x\)
+) Số thứ nhất sau khi chia cho 9 gọi là \(\dfrac{x}{9}\)
Số thứ hai sau khi chia cho 6 gọi là \(\dfrac{\dfrac{3}{5}x}{6}\)
Vì: thương số thứ nhất chia cho 9 bé hơn thương số thứ hai chia cho 6 là 3 đơn vị nên ta có phương trình:
\(\dfrac{x}{9}+3=\dfrac{\dfrac{3}{5}x}{6}\\ < =>\dfrac{2x}{18}+\dfrac{54}{18}=\dfrac{\dfrac{9}{5}x}{18}\\ < =>2x+54=\dfrac{9}{5}x\\ < =>2x-\dfrac{9}{5}x=-54\\< =>\dfrac{1}{5}x=-54\\ =>x=\dfrac{-54}{\dfrac{1}{5}}=-270\left(loại\right)\)
Vậy: Không thỏa mãn yêu cầu đề bài.

Gọi 2 số cần tìm lần lượt là a, b \(\left(a,b\inℕ^∗\right)\)
Tỉ số giữa số thứ nhất và số thứ 2 là \(\frac{4}{7}\)\(\Rightarrow\frac{a}{b}=\frac{4}{7}\)\(\Rightarrow\frac{a}{4}=\frac{b}{7}\)
Đặt \(\frac{a}{4}=\frac{b}{7}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=4k\)và \(b=7k\)
Nếu lấy số thứ nhất chia cho 4, số thứ 2 chia cho 5 thì thương số thứ nhất bé hơn thương thứ hai 2 đơn vị
\(\Rightarrow\)Ta có phương trình: \(\frac{7k}{5}-\frac{4k}{4}=2\)
\(\Leftrightarrow\frac{28k}{20}-\frac{20k}{20}=\frac{40}{20}\)\(\Leftrightarrow8k=40\)\(\Leftrightarrow k=5\)( thoả mãn điều kiện )
\(\Rightarrow a=4.5=20\); \(b=5.7=35\)
Vậy số bé là 20 và số lớn là 35
gọi hai số đó là x và y. ta có
\(\hept{\begin{cases}\frac{x}{y}=\frac{9}{20}\\\frac{y}{4}-\frac{x}{3}=4\end{cases}\Rightarrow x=\frac{9}{20}y}\Rightarrow\frac{y}{4}-\frac{9y}{20.3}=4\Leftrightarrow y=40\Rightarrow x=18\)