Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng lí thuyết về giao thoa sóng hai nguồn cùng pha và áp dụng công thức tính số cực đại trên đoạn thẳng nối hai nguồn
Cách giải:
Hình ảnh giao thoa:
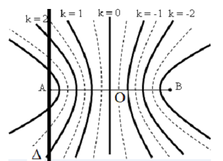
+ Số cực đại trên đoạn AB bằng số giá trị k nguyên thoả mãn:
− A B λ < k < A B λ ⇔ − 16 3 < k < 16 3 ⇔ − 5,3 < k < 5,3 ⇒ k = 0 ; ± 1 ; ... ; ± 5
+ Trong khoảng từ A đến O có 5 đường hypebol cực đại. Mỗi đường cắt ( ∆ ) tại 2 điểm ⇒ Trên ( ∆ ) có 10 điểm dao động với biên độ cực đại

Đáp án C

+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:

+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
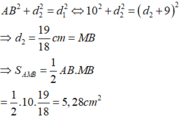

Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
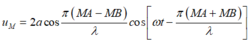
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
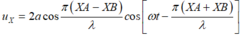
Vì X và M thuộc elip => M + MB = X + XB

=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M

Đáp án B
Với hiện tượng giao thoa hai nguồn kết hợp cùng pha thì trung điểm của đoạn thẳng nối hai nguồn là một cực đại

Hai cực đại liên tiếp cách nhau một đoạn: λ/2=1,5cm→λ=3cm
Tốc độ truyền sóng:v=λf=3.40=120cm/s=1,2m/s
Chọn đáp án C

Đáp án C
Phương pháp: Δ φ = 2 π d λ
Cách giải:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
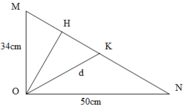
1 O H 2 = 1 O M 2 + 1 O N 2 ⇔ 1 O H 2 = 1 34 2 + 1 50 2 ⇒ O H = 28,1 c m
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là: Δ φ = 2 π d λ
+ Để K dao động cùng pha với O thì: Δ φ = 2 π d λ = 2 k π ⇒ d = k λ
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn:
28,1 ≤ k λ ≤ 34 ⇒ 7,025 ≤ k ≤ 8,5 ⇒ k = 8 28,1 < k λ ≤ 50 ⇒ 7,025 < k ≤ 12,5 ⇒ k = 8 ; 9 ; 10 ; 11 ; 12
Có 6 giá trị của k thoả mãn ⇒ trên đoạn MN có 6 điểm dao động cùng pha với nguồn



Chọn đáp án C