Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
x M = 2 A cos d 2 − d 1 λ π cos ( ω t − d 2 + d 1 λ π ) .Vì M và N thuộc elip → d 1 + d 2 = const;
do M và N thuộc hai cực đại liên tiếp nên d 1 + d 2 = kλ .
Nếu k chẵn đối với M thì x M = 2 A cos ( ω t − d 2 + d 1 λ π ) ;
x N = − 2 A cos ( ω t − d 2 + d 1 λ π ) .
Nếu k lẻ đối với M thì x M = − 2 A cos ( ω t − d 2 + d 1 λ π ) ; x N = 2 A cos ( ω t − d 2 + d 1 λ π )
→ M và N ngược pha.

Đáp án A.
Lời giải chi tiết:
Độ lệch pha của điểm M với hai nguồn là 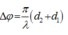
Điều kiện để M lệch pha π 2 so với nguồn:
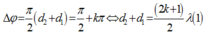
Vậy quỹ tích các điểm lệch pha π 2 so với nguồn là đường elip thỏa mãn đều kiện (1) nhận S1 và S2 làm tiêu điểm.
+ Điều kiện để các đường elip này nằm trong (E) là:
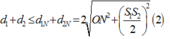
+ Mặt khác tổng các cạnh trong một tam giác lớn hơn cạnh còn lại nên
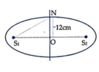
![]()
Kết hợp (1), (2) và (3) ta có:
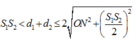
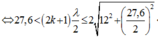

Vậy có 2 đường elip nằm trong € mà các điểm trên đó lệch pha π 2 so với nguồn.
+ Số điểm giao động với biên độ cực đại trên đoạn thẳng nối hai nguồn:
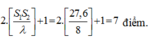
+ Vì 1 đường cực đại cắt elip tại 2 điểm nên trên 1 đường elip có 14 điểm dao động với biên độ cực đại.
Vậy trên 2 đường elip có 28 điểm dao động với biên độ cực đại và lệch pha π 2 số với nguồn.

Chọn đáp án B
Đặt A B = l = 50 c m , bước sóng λ = v . T = 8 c m .
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
− l λ < k < l λ ⇒ − 6,25 < k < 6,25 ⇒ k = 0, ± 1,...., ± 6.
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒MA = MB + 48 (cm). MB⊥AB
⇒ M A 2 = A B 2 + M B 2 ⇔ ( M B + 48 ) 2 = A B 2 + M B 2 ⇔ M B 2 + 96 M B + 48 2 = 50 2 + M B 2 ⇔ M B = 50 2 − 48 2 96 = 2,04 c m

Đáp án B
Đặt AB =l = 50 cm, bước sóng λ = v.T = 8cm.
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
- 1 λ < k < 1 λ ⇒ - 6 , 25 < k < 6 , 25 ⇒ k = 0 , ± 1 , . . . , ± 6
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒ MA = MB + 48 (cm). MB⊥AB
⇒ MA 2 = AB 2 + MB 2 ⇔ ( MB + 48 ) 2 = AB 2 + MB 2 ⇔ MB 2 + 96 MB + 48 2 = 50 2 + MB 2 ⇔ MB = 50 2 - 48 2 96 = 2 , 04 cm

Đáp án B
Ta có λ = v f = 1 50 = 0 , 02 ( m ) = 2 c m
Hai điểm gần nhất dao động ngược pha cách nhau λ 2 = 1 c m

Đáp án D
![]()
Độ lệch pha giữa M và O:
![]() ;
;
điểm dao động với biên độ cực tiểu trên AB thỏa mãn ![]()
Điểm N dao động với biên độ cực tiểu và gần A nhất suy ra:
![]() = 7,5
= 7,5
Suy ra:
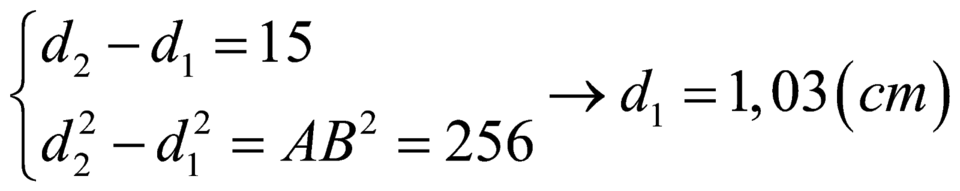

- Gọi d1, d2 là khoảng cách từ M đến 2 nguồn (M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông
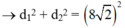
+ M dao động với biên độ cực đại nên: d1 - d2 = kλ
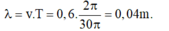
- Giải hệ phương trình trên ta được:
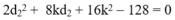
+ Chỉ có k = 0 là thỏa mãn ⇒ d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên:
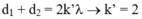
- Vậy có tất cả 2 điểm.

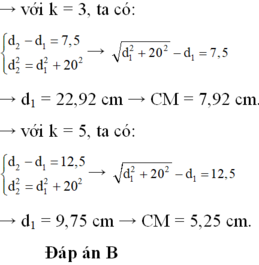

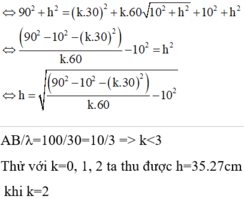
Đáp án C
x M = 2 A cos d 2 - d 1 λ π cos ( ω t - d 2 + d 1 λ π ) . Vì M và N thuộc elip → d1 + d2 = const;
do M và N thuộc hai cực đại liên tiếp nên d2 − d1 = kλ .
Nếu k chẵn đối với M thì x M = 2 A cos ( ω t - d 2 + d 1 λ π ) ; x N = - 2 A cos ( ω t - d 2 + d 1 λ π )
Nếu k lẻ đối với M thì x M = - 2 A cos ( ω t - d 2 + d 1 λ π ) ; x N = 2 A cos ( ω t - d 2 + d 1 λ π )
→ M và N ngược pha.