Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Góc \(\varphi \) và góc \(\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\) có thể bằng nhau hoặc bù nhau.
b) Do góc \(\varphi \) và góc \(\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\) có thể bằng nhau hoặc bù nhau nên \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\)

Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.
Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.

a) Tọa độ giao điểm của hai đường thẳng \({\Delta _1};{\Delta _2}\)là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\sqrt 3 x + y - 4 = 0\\x + \sqrt 3 y - 2\sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt 3 \\y = 1\end{array} \right.\)
b) Ta có: \(\cos \left( {{\Delta _1};{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2} \Rightarrow \left( {{\Delta _1};{\Delta _2}} \right) = {30^o}\)
Vậy số đo góc giữa hai đường thẳng \({\Delta _1};{\Delta _2}\) là \({30^o}\).

a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\)
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)

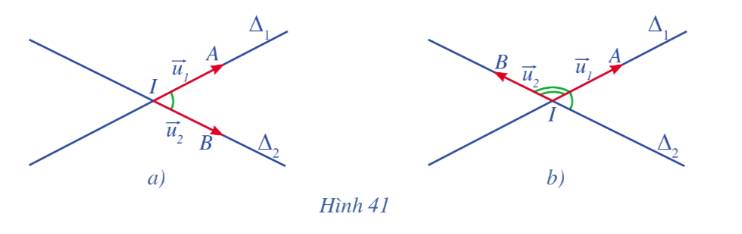
a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)có thể bẳng nhau hoặc bù nhau.
b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).
Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).
Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\)

a) - Ta có: \(\overrightarrow {{u_1}} = \left( {3\sqrt 3 ;3} \right);\overrightarrow {{u_2}} = \left( {1 ;0} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {3\sqrt 3 .1 + 3.0} \right|}}{{\sqrt {{{\left( {3\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{{\sqrt 3 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\)
b) – Ta có\(\overrightarrow {{n_1}} = \left( {2; - 1} \right);\overrightarrow {{n_2}} = \left( { - 1 ;3} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.\left( { - 1} \right) + \left( { - 1} \right).3} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( 1 \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}.\)
- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)

Vecto pháp tuyến của là: \(\overrightarrow {{n_1}} = \left( {m; - 1} \right)\)
Vecto pháp tuyến của là: \(\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Vậy ai đường thẳng \({\Delta _1}\),\({\Delta _2}\) vuông góc với nhau khi và chỉ khỉ \(\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} \) vuông góc với nhau tức là \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow 2m + 1 = 0 \Leftrightarrow m = \frac{{ - 1}}{2}\)

Ta có \({\Delta _1}\)có vecto pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1;3} \right)\).
Phương trình tổng quát của \({\Delta _2}\) là \(3x - y + 1 = 0\), suy ra \(\overrightarrow {{n_2}} = \left( {3; - 1} \right)\)
Do \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.3 + 3.\left( { - 1} \right) = 0\). Vậy hai đường thẳng vuông góc với nhau.
Cách 2:
Gọi \(\varphi \) là góc giữa hai đường thẳng, ta có:
\(\cos \varphi = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {1.3 + 3.( - 1)} \right|}}{{\sqrt {{1^2} + {3^2}} .\sqrt {{3^2} + {{( - 1)}^2}} }} = 0\)
Do đó góc giữa \({\Delta _1}\) và \({\Delta _2}\) là \(\varphi =90^o\)

a) Đường thẳng \({\Delta _1}\)có một vectơ chỉ phương là \({\overrightarrow u _{{\Delta _1}}} = \left( {2;5} \right)\)
Do đó \({\overrightarrow n _{{\Delta _1}}} = \left( { - 5;2} \right)\), đồng thời \({\Delta _1}\) đi qua điểm \(M\left( {1;3} \right)\) nên phương trình tổng quát của \({\Delta _1}\) là: \(-5\left( {x - 1} \right) + 2\left( {y - 3} \right) = 0 \Leftrightarrow 5x - 2y + 1 = 0\).
b) Đường thẳng \({\Delta _2}\)có một vectơ pháp tuyến là \({\overrightarrow n _{{\Delta _2}}} = \left( {2;3} \right)\)
Do đó \({\overrightarrow u _{{\Delta _1}}} = \left( { - 3;2} \right)\), đồng thời \({\Delta _2}\) đi qua điểm \(N\left( {1;1} \right)\) nên phương trình tham số của \({\Delta _2}\) là: \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 1 + 2t\end{array} \right.\).
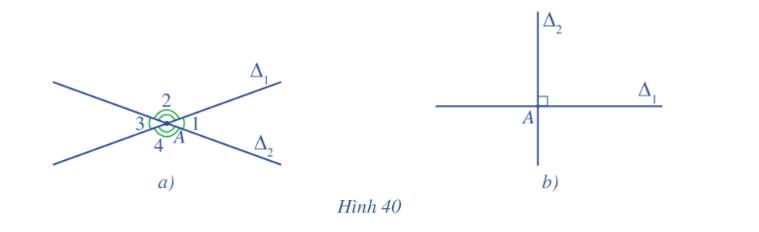
Hai đường thẳng cắt nhau tạo thành bốn góc trong đó có hai góc nhọn bằng nhau và hai góc tù bằng nhau. Góc nhọn và góc tù trong trường hợp này là hai góc bù nhau.