
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#)Giải :
Vì \(\widehat{AOC}\) và \(\widehat{AOD}\)là hai góc kề bù
\(\Rightarrow\widehat{AOC}+\widehat{AOD}=180^o\)
\(\Rightarrow\widehat{AOC}=\frac{\left(180^o+20^o\right)}{2}=100^o\)
\(\Rightarrow\widehat{AOD}=100^o-20^o=80^o\)
\(\Rightarrow\widehat{COB}=\widehat{AOD}=80^o\)(hai góc đối đỉnh)
\(\Rightarrow\widehat{BOD}=\widehat{AOC}=100^o\)(nt)

Ta có :
aÔc = 3 bÔc
aÔc + bÔc = 180o ( 2 góc kề bù)
=> 3bÔc + bÔc = 180o
4bÔc = 180o
bÔc=45o
aÔc = 3 . 45o =135o
aÔc = bÔd = 135o ( đối đỉnh )
bÔc = aÔd = 45o ( đối đỉnh)

góc AOC=3*góc BOC
góc AOC+góc BOC=180 độ
=>góc AOC=3/4*180=135 độ; góc BOC=180-135=45 độ
góc AOD=góc BOC=45 độ
góc BOD=góc AOC=135 độ

Ta có :
aÔc = 3 bÔc
aÔc + bÔc = 180o ( 2 góc kề bù)
=> 3bÔc + bÔc = 180o
4bÔc = 180o
bÔc=45o
aÔc = 3 . 45o =135o
aÔc = bÔd = 135o ( đối đỉnh )
bÔc = aÔd = 45o ( đối đỉnh)


TH1: \(\widehat{AOC}+\widehat{AOD}+\widehat{BOD}=230o\)
Mà \(\widehat{AOC}=\widehat{BOD}\) (2 góc đối đỉnh)
=> \(2.\widehat{AOC}+\widehat{AOD}=230o\)
Mà \(\widehat{AOC}+\widehat{AOD}=180o\) (2 góc kề bù)
=> \(\left\{{}\begin{matrix}\widehat{AOC}=\widehat{BOD}=50o\\\widehat{AOD}=\widehat{BOC}=130o\end{matrix}\right.\)
TH2: \(\widehat{AOD}+\widehat{BOD}+\widehat{BOC}=230o\)
Mà \(\widehat{AOD}=\widehat{BOC}\) (2 góc đối đỉnh)
=> \(2.\widehat{AOD}+\widehat{BOD}=230o\)
Mà \(\widehat{AOD}+\widehat{BOD}=180o\)
=> \(\left\{{}\begin{matrix}\widehat{AOD}=\widehat{BOC}=50o\\\widehat{BOD}=\widehat{AOC}=130o\end{matrix}\right.\)
vô lí do \(\widehat{AOC}>\widehat{BOC}\)
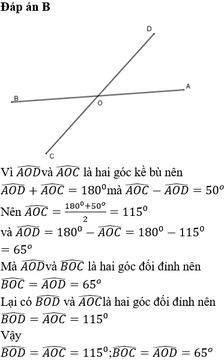
Ta có
AB cắt CD tại O=>AOC+AOD=180O (1)
Lại có AOC-AOD=50O (2)
Từ (1),(2)=>AOD=(180O-50O):2=65O
Từ (1)=>AOD=BOC(2 góc đối đỉnh)
=>BOC=65O
CHÚC BẠN HỌC TỐT
DẤU NGANG ĐÓ KÍ HIỆU LÀ GÓC NHÉ