Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+ Pha dao động của chất điểm khi t = 1 s là 1,5π rad.
Đáp án D
Xét dao động (2). Tại t=0 vật đang ở biên dương, đến thời điểm t = 0,5 s vật đi qua vị trí cân bằng theo chiều âm
=> 0,25T =0,5 => T = 2s → ω = π rad / s → x 2 = 6 cosπt
Xét dao động (1), tại t=0, vật đi qua vị trí x = +0,5A = 2 cm theo chiều dương
→ x 1 = 4 cos ( πt - π 3 ) c m
Bấm máy ta dễ dàng tìm phương trình dao động thứ hai
x = x 2 - x 1 = 2 7 cos ( πt + 0 , 714 ) c m
Chọn A
+ Hai dao động cùng pha
và pha φ là pha của các dao động
=> x = 15cos(πt + π/6)cm.
Đáp án C
Có thể bấm nhanh bằng máy tính:
Vậy dao động thứ 2 có phương trình li độ: x 2 = 8 cos ( π t - 5 π 6 ) ( c m )
Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ
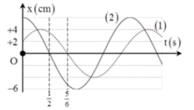
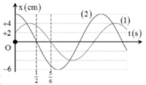
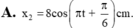
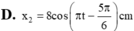
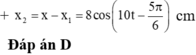
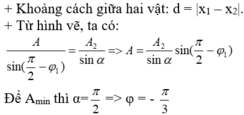
- Xét dao động (2). Tại t = 0 vật đang ở biên dương, đến thời điểm t= 0,5s vật đi qua vị trí cân bằng theo chiều âm
- Xét dao động (1), tại , vật đi qua vị trí x = +0,5A = 2cm theo chiều dương:
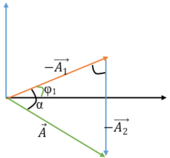
- Phức hóa, để tìm phương trình dao động thứ hai: