Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do hai con chim vồ mồi cùng 1 lúc và với cùng một vận tốc nên quãng đường bay của 2 con pải như nhau
Gọi khoảng cách của con cá tới 2 gốc cây lần lượt là x,y(x,y>0)
Khoảng cách bay của con 1 là : \(\sqrt{20^2+x^2}\)\
Khoảng cách bay của con thứ 2 là \(\sqrt{30^2+y^2}\)
Do khoảng cách bằng nhau nên ta có pt:
\(\sqrt{30^2+y^2}=\sqrt{20^2+x^2}\)
\(\Leftrightarrow500=x^2-y^2=\left(x+y\right)\left(x-y\right)\)
\(\Leftrightarrow500=50\left(x-y\right)\)(do x+y=50)
\(\Leftrightarrow x-y=10\)
\(\Rightarrow\hept{\begin{cases}x+y=50\\x-y=10\end{cases}\Rightarrow x=30,y=20}\)
Vậy con trên cây cao 30 m có gốc cây cách con cá 20m
con trên cây cao 20m có gốc cây cách con cá 30m

Do hai con chim vồ mồi cùng 1 lúc và với cùng một vận tốc nên quãng đường bay của 2 con pải như nhau
Gọi khoảng cách của con cá tới 2 gốc cây lần lượt là x,y(x,y>0)
Khoảng cách bay của con 1 là : \(\sqrt{20^2+x^2}\)\
Khoảng cách bay của con thứ 2 là \(\sqrt{30^2+y^2}\)
Do khoảng cách bằng nhau nên ta có pt:
\(\sqrt{30^2+y^2}=\sqrt{20^2+x^2}\)
\(\Leftrightarrow500=x^2-y^2=\left(x+y\right)\left(x-y\right)\)
\(\Leftrightarrow500=50\left(x-y\right)\)(do x+y=50)
\(\Leftrightarrow x-y=10\)
\(\Rightarrow\hept{\begin{cases}x+y=50\\x-y=10\end{cases}\Rightarrow x=30,y=20}\)
Vậy con trên cây cao 30 m có gốc cây cách con cá 20m
con trên cây cao 20m có gốc cây cách con cá 30m

mk nghĩ là nếu đố mẹo thif vẫn sẽ có 1 con tại vì đề bài có nói là bay đến cành cây đó đâu
ko đố mẹo thì có 101 con

có 3 con
có 1 con chim
bà là bố con chim là 1 con
tỉ tỉ là chị con chim là 1 con
Vậy tổng cộng là 3 con

Dịch lại đề toán (lẫn cả tiếng miền nam và tiếng Trung quốc nên các bạn khó hiểu)
3 = ba = bố
tỉ tỉ = chị
Như vậy đề toán sẽ là: Trên cành cây có 1 con chim và có bố con chim bay đến và chị con chim bay đến, hỏi trên cành cây có bao nhiêu con chim?
Đáp số: 3 con chim.

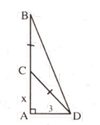
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
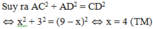
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C


Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x CB = CD = 8 – x.
Vì ∆ ACD vuông tại A
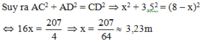
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B