Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

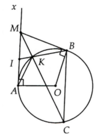
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
b: Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=60^0\)
Xét ΔMAB có MA=MB và \(\widehat{AMB}=60^0\)
nên ΔMAB đều
c: Xét (O) có
CA,CP là các tiếp tuyến
Do đó: CA=CP và OC là phân giác của góc AOP
Xét (O) có
DB,DP là các tiếp tuyến
Do đó; DB=DP và OD là phân giác của góc BOP
ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=\left(2R\right)^2-R^2=3R^2\)
=>\(AM=R\sqrt{3}\)
Chu vi tam giác MCD là:
\(C_{MCD}=MC+CD+MD\)
\(=MC+CP+MD+DP\)
\(=MC+CA+MD+DB\)
=MA+MB=2MA=\(=R\sqrt{3}\cdot2=2R\sqrt{3}\)
d: Ta có: OC là phân giác của góc AOP
=>\(\widehat{AOP}=2\cdot\widehat{COP}\)
Ta có: OD là phân giác của góc BOP
=>\(\widehat{BOP}=2\cdot\widehat{DOP}\)
Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}=120^0\)
Ta có: \(\widehat{AOP}+\widehat{BOP}=\widehat{AOB}\)
=>\(2\cdot\left(\widehat{COP}+\widehat{DOP}\right)=120^0\)
=>\(2\cdot\widehat{COD}=60^0\cdot2\)
=>\(\widehat{COD}=60^0\)
M A C D B O K N E F H I
a/
Ta có A và B cùng nhìn MO dưới 1 góc vuông => B và B thuộc đường tròn đường kính MO => A, B, M, O cùng nằm trên 1 đường tròn
b/
Ta có
\(C_{MCD}=MC+MD+CD=\left(MC+NC\right)+\left(MD+ND\right).\)
Ta có
MA = MB (hai tiếp tuyến cùng xp từ 1 điểm)
NC=AC; ND = BD (hai tiếp tuyến cùng xp từ 1 điểm)
\(\Rightarrow C_{MCD}=\left(MC+AC\right)+\left(MD+BD\right)=MA+MB=2MA\)
M cố định; A cố định => MA không đổi \(\Rightarrow C_{MCD}=2MA\) không đổi => \(C_{MCD}\) không phụ thuộc vị trí điểm N
c/
Xét tg vuông NOC và tg vuông AOC có
OC chung
NC = AC (cmt)
\(\Rightarrow\Delta NOC=\Delta AOC\) (hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{OCA}=\widehat{OCD}\) (1)
Gọi P là giao OC với (O) và Q là giao của OD với (O)
Ta có
sđ cung AP = sđ cung NP; sđ cung BQ = sđ cung NQ (hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn chia đôi cung giới hạn bởi hai tiếp điểm)
=> sđ cung NP = 1/2 sđ cung AN; sđ cung NQ = 1/2 sđ cung BN
=> sđ cung NP + sđ cung NQ = sđ cung PQ = 1/2 sđ cung AN + 1/2 sđ cung BN = 1/2 sđ cung AB
\(\Rightarrow\widehat{COD}=sđ\) cung PQ = 1/2 sđ cung AB (góc ở tâm)
Ta có \(\widehat{CAB}=\)1/2 sđ cung AB (góc giữa tiếp tuyến và dây cung)
\(\Rightarrow\widehat{CAB}=\widehat{COD}\) (2)
Xét tg CKA và tg ODC có
\(\widehat{OCA}=\widehat{OCD;}\widehat{CAB}=\widehat{COD}\) => tg CKA đồng dạng với tg ODC (g.g.g)
d/
Gọi I là giao của EF với MA
Xét tg OAB và tg OEF có
OA = OE; OB = OF (đều là bán kính (O))
\(\widehat{AOB}=\widehat{EOF}\) (góc đối đỉnh)
\(\Rightarrow\Delta OAB=\Delta OEF\left(c.g.c\right)\Rightarrow\widehat{BAO}=\widehat{IEO}\) => AB // EF (hai đường thẳng bị cắt bởi 1 đường thẳng tạo thành 2 góc so le trong = nhau thì // với nhau)
Ta có \(MO\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn vuông góc với dây cung nối 2 tiếp điểm)
\(\Rightarrow MO\perp EF\) (đường thẳng vuông góc với 1 trong 2 đường thẳng // với nhau thì cũng vuông góc với đường thẳng còn lại)
Xét \(\Delta MIE\) có
\(EA\perp MI;MO\perp EF\) => O là trực tâm của tg MIE => OH là đường cao thuộc cạnh ME => OH phải đi qua I => EF; MA; OH đồng quy tại I