Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau khoảng thời gian \(\tau\) thì số hạt nhân còn lại là
\(N = N_0 2^{-\frac{\tau}{T}}\)
=> \(\frac{N}{N_0}= \frac{1}{4}= 2^{-2}= 2^{-\frac{\tau}{T}}\)
=> \(\tau = 2T.\)
Sau khoảng thời gian \(2\tau\) thì số hạt còn lại là
\(N_1 = N_02^{-\frac{2\tau}{T}}= N_0.2^{-\frac{4T}{T}}= \frac{1}{16}N_0\)
=> Số hạt còn lại chiếm 6,25 % số hạt ban đầu.

Đề bài sửa lại như sau:
Gọi Δt là khoảng thời gian để số hạt nhân của một lượng chất phóng xạ giảm đi e lần (e là cơ số của loga tự nhiên với lne = 1), T là chu kỳ bán rã của chất phóng xạ. Hỏi sau khoảng thời gian 0,51Δt chất phóng xạ còn lại bao nhiêu phần trăm lượng ban đầu?
Bài giải:
Theo bài, sau Δt thì số hạt nhân giảm e lần, tức là
Tỉ lệ số hạt nhân còn lại so với ban đầu là 60%.
Vậy đáp số là 60%
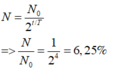

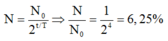
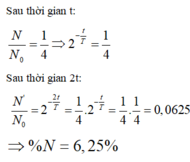
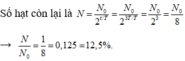
Đáp án C