Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp :
Tìm nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 bằng MTCT.
Cách giải:
Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là
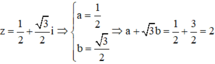

Đáp án C
z 2 + b z + a 2 + 4 = 0 ⇒ a 2 − b 2 + 2 a b i + a b + b 2 i + a 2 + 4 = 0 ⇒ 2 a 2 − b 2 + a b + 4 + ( 2 a b + b 2 ) i = 0 ⇒ 2 a 2 − b 2 + a b + 4 = 0 2 a b + b 2 = 0 · b = 0 ⇒ 2 a 2 + 4 = 0 ( V N ) · b = − 2 a ⇒ 2 a 2 − 4 a 2 − 2 a 2 + 4 = 0 ⇔ a = ± 1 ⇒ b = ∓ 2 ⇒ z = 5

Đáp án C
z 2 + b z + a 2 + 4 = 0 ⇒ a 2 - b 2 + 2 a b i + a b + b 2 i + a 2 + 4 = 0 ⇒ 2 a 2 - b 2 + a b + 4 + 2 a b + b 2 i = 0 ⇒ 2 a 2 - b 2 + a b + 4 = 0 2 a b + b 2 = 0 b = 0 ⇒ 2 a 2 + 4 = 0 ( V N ) b = - 2 a ⇒ 2 a 2 - 4 a 2 - 2 a 2 + 4 = 0 ⇔ a = ± 1 ⇒ b = ∓ 2 ⇒ z = 5

Chọn A
Gọi (P) là mặt phẳng qua A chứa
![]()
Tìm ra toa độ điểm B, sau đó viết phương trình đường thẳng d qua A, B
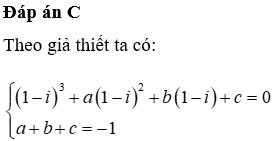
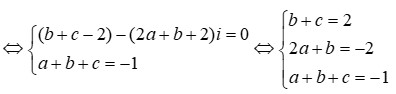
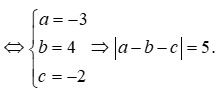

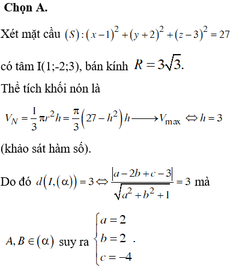
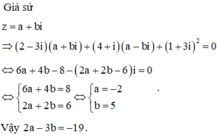


Chọn D