Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 6x – 7y = 5 ⇔ x = 7 y + 5 6 ⇔ x = y + y + 5 6
Đặt y + 5 6 = t t ∈ ℤ ⇒ y = 6t – 5 = 6 ⇒ x = y + y + 5 6 = 6t – 5 + t = 7t – 5
Nên nghiệm nguyên của phương trình là x = 7 t − 5 y = 6 t − 5 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 7 t − 5 > 0 6 t − 5 > 0 ⇒ t > 5 7 t > 5 6 ⇒ t > 5 7
mà t ∈ ℤ ⇒ t ≥ 1
Do đó nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1
⇒ x = 7.1 − 5 y = 6.1 − 5 ⇒ x = 2 y = 1 ⇒ x − y = 1
Đáp án: C

a)
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | \(\sqrt{22}\)(loại | \(2\sqrt{7}\)(loại) | \(\sqrt{46}\)(loại) | 10(thoả mãn) | \(\sqrt{262}\) |
\(\Rightarrow\left(x,y\right)=\left(4;10\right)\)

a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
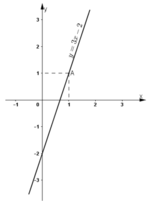
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
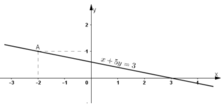
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 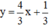
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
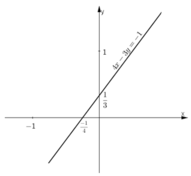
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
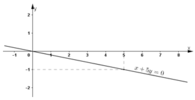
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 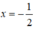
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
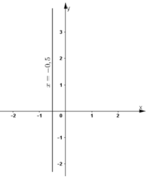
f) 0x + 2y = 5
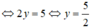
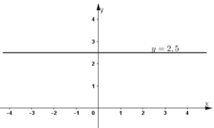
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.

ĐK: x ≥ 0; y ≥ 0
Ta có
4 x − 3 y = 4 2 x + y = 2 ⇔ 4 x − 3 y = 4 4 x + 2 y = 4 ⇔ 5 y = 0 2 x + y = 2 ⇔ y = 0 2 x = 2
⇔ y = 0 x = 1 (Thỏa mãn)
Vậy hệ phương trình có 1 nghiệm duy nhất (x; y) = (1; 0) ⇒ x.y = 0
Đáp án: B

Điều kiện: x ≥ 0; x ≠ 7; y ≥ 0
Đặt 1 x − 7 = a ; 1 y + 6 = b ta được 7 a − 4 b = 5 3 5 a + 3 b = 2 1 6 ⇔ 21 a − 12 b = 5 20 a + 12 b = 26 3
21 a − 12 b = 5 41 a = 41 3 ⇔ a = 1 3 21. 1 3 − 12 b = 5 ⇔ a = 1 3 b = 1 6
Trả lại biến ta có
1 x − 7 = 1 3 1 y + 6 = 1 6 ⇔ x − 7 = 3 y + 6 = 6 ⇔ x = 100 y = 0 T M
Vậy hệ phương trình có nghiệm (x; y) = (100; 0)
Đáp án: D
Ta có −4x + 3y = 8 ⇔ y = 4 x + 8 3 ⇔ y = x + x + 8 3
Đặt x + 8 3 = t ⇒ x = 3t – 8 ⇒ y = 3t – 8 + t ⇒ y = 4t – 8 ( )
Nên nghiệm nguyên của phương trình là x = 3 t − 8 y = 4 t − 8 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 3 t − 8 > 0 4 t − 8 > 0 ⇒ t > 8 3 t > 2 ⇒ t > 8 3
mà t ∈ ℤ ⇒ t ≥ 3
Nghiệm nguyên dương nhỏ nhất của phương trình là x = 3.3 − 8 y = 4.3 − 8 ⇔ x = 1 y = 4
⇒ x + y = 5
Đáp án: A