Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C

a/ Ta có: QP vuông góc với AM tại P (gt) (1)
AB vuông góc với AM tại A(do Ax là tiếp tuyến của (O) tại A) (2)
Từ (1) và (2)=> QP//AB (3)
Mà: AP=PM=1/2 AM (gt)(4)
Từ (3) và (4)=>QP là đường trung bình trong tam giác ABM
=> QB=QM=1/2 BM (5)
Mà OB=OA (=R) (6)
Từ (5) và (6)=>OQ là đường trung bình trong tam giác ABM
=>OQ//AM (7)
Từ (2) và (7)=>góc BOQ=90 độ (=góc BAM)(8)
Tứ giác BNAC nội tiếp (O)
=> góc BCN=góc BAN (9)
Mà góc BAN+ góc ABN=90 độ (tam giác BOQ vuông do góc QOB=90 độ) (10)
Từ (9) và (10)=> góc BCN+góc ABN=90 độ (11)
Lại có: góc ABN + góc BQO= 90 độ (Tam giác BOQ vuông) (12)
Từ (11) và (12)=> góc BCN=góc BQO
hay góc BCN=góc OQN (do B, N, Q thẳng hàng) (đpcm)

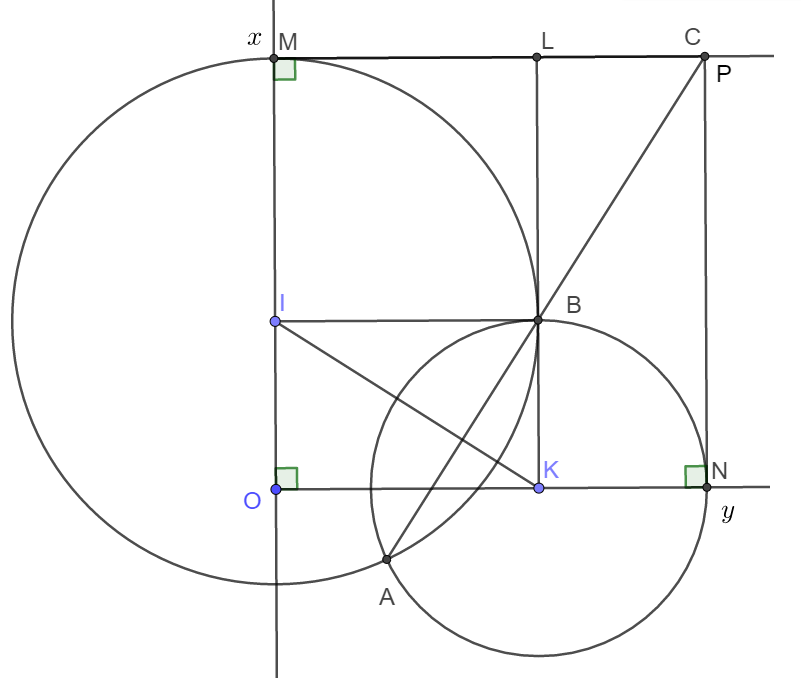
a) Trong tam giác OIK có:
|OK OI| < IK < |OK + OI| hay .
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra . Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.

a.
Góc AKB là góc nội tiếp chắn nửa (O) nên ∠AKB=90o∠AKB=90o
Khi này dễ dàng có đpcm
b.
Do C là trung điểm OA nên AC=OA2=R2AC=OA2=R2
Tứ giác BCHK nội tiếp nên chứng minh được △AHC∼△ABK△AHC∼△ABK
Từ đó: ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2
c.
Lấy điểm E trên tia đối của BK sao cho KE=KM=KI
Chứng minh được tam giác AMO đều (có 3 cạnh = nhau) khi đó ∠MAB=60o∠MAB=60o
Dễ dàng chứng minh được tứ giác ABKM nội tiếp nên ∠MKE=∠MAB=60o∠MKE=∠MAB=60o
khi đó tam giác MKE đều nên ME = MK(1)
Có ∠CMB=∠MAB=6oo∠CMB=∠MAB=6oo (hai góc cùng phụ với góc AMC) nên
∠MNK=∠BME(2)∠MNK=∠BME(2)
Góc CMB=60oCMB=60o nên MB=2MCMB=2MC mà MN=2MCMN=2MC nên MN=MB(3)MN=MB(3)
Từ (1),(2) và (3) nên △NMK=△BME△NMK=△BME nên NK=BENK=BE hay NI+IK=BK+KINI+IK=BK+KI từ đó có đpcm
Hình gửi kèm

Mình chép lại cái đề cho trắc nè
Gọi M và N là 2 điểm khác phía với đường xy. MN cắt xy tại O. Trên tia Ox lấy A sao cho : OA=2.
a) Giả sử MAx=NAx=1200. Chứng minh Ay phân giác MAN
b) Trên Oy lấy B, giả sử MBN=1000;MBO=400. Tính OBN
c)Muốn cho O trung điểm AB thì OB phải bằng bao nhiêu ?
dài lắm . ghi mỏi tay . chiều rùi mink sẽ ve cho thằg lộc