Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M A N B D C E F
a, bn dựa vào hình nha
b,bn kham khảo trên h
c, Vì EFKH là hinhg bình hành nên để EFKH là hình chữ nhật thì EH⊥EF
Nối AG.
Ta lại có: EH//AG (EH là đường TB)
Và EH⊥EF EF⊥AG AG⊥BC (EF//BC)
mà ta đã có AG là đường trung tuyến của ΔABC
ΔABC cân tại A
Vâỵ để EFKH là hình chữ nhật thì tam giác ABC phải cân tại A.
Kéo dài AG cắt BC tại I
Khi đó SEFKH=EH.EF=12AG.12BC=14.23AI.BC=16AI.BC
Và SABC=BC.AI (vì ta đã CM được AI là đường cao)
SEFKHSABC=16AI.BCBC.AI=16
Vậy SEFKH=16SABC
Những gì mình làm chỉ có vậy thôi chúc bn hc tốt
A B C E F K H G
a) E là trung điểm AB, F là trung điểm AC
=> EF là đường trung bình của tam giác ABC
=> EF//BC
=> EFCB là hình bình hành
b) H là trung điểm BG, K là trung điểm CG
=> HK là đường trung bình của tam giác GBC
=> HK//=\(\frac{1}{2}\)BC
mà EF//=\(\frac{1}{2}\) BC ( vì EF là đường trung bình của tam giác ABC )
=> HK//=EF
=> HKEF là hình bình hành
c) Để EFHK là hình chữ nhật
ĐK là HE vuông EF (1)
Vì H là trung điểm BG
E là trung điểm AB
=> HE là đường trung bình BAG
=> EH//AG (2)
mà EF//BC (3)
1, 2, 3 => AG vuông BC (4)
Mặt khác G là giao điểm 2 đường trung tuyến CE, BFcủa tam giác ABC
=> G là trọng tâm
=> AG là đường trung tuyến (5)
4, 5 => Tam giác ABC cân tại A
Vậy để EFKH là hình chữ nhật thì tam giác ABC cân tại A
Gọi M là giao điểm của BC
=> Diện tích tam giác ABC :=\(\frac{1}{2}\)AM. BC
Diện tích EFKH := EF.EH=\(\frac{1}{2}\)BC.\(\frac{1}{2}\)AG=\(\frac{1}{2}\)BC. \(\frac{1}{2}\).\(\frac{2}{3}\) AM=\(\frac{1}{6}\)AM.BC =\(\frac{1}{3}\)diện tíc ABC
=> Tự so sánh nhé!

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC và EF=BC/2(1)
hay EFCB là hình thang
b: Xét ΔGBC có
K là trung điểm của GB
H là trung điểm của GC
Do đó: KH là đường trung bình
=>KH//BC và KH=BC/2(2)
Từ (1) và (2) suy ra EF=HK và EF=HK
hay EFKH là hình bình hành

1A) Gọi I là giao điểm của EF và AB Vì EF là đường trung trực của MB nên BE=BF xét hai tam giác BEI và BFI thì chúng bằng nhau ( t. hợp ch-cgv) IE=IF; EF vuông góc AB =) E và F đối xứng nhau qua AB nên ta chứng minh được hai tam giác BEI và BF1 bằng nhau. 1b) gọi I là giao điểm của MB và EF
ta có EI là đường trung bình của tam giác MEB
nên tam giác MEB cân tại E => góc EMB = góc EBM
có EI là đường cao đồng thời là đường phân giác
nên góc MEI = góc BEI
ta có MN//BC//AD
hay ME//BF
nên góc MFI = góc IFB; góc EMB = góc FBM ( 2 góc slt)
mà góc MEI = góc BEI
nên góc IFB = góc BEI
=> tam giác BEF cân tại B
lại có BI là tia phân giác (góc EBI = góc FBI=góc EMI)
hay BI là đường trung tuyến
ta có EF vuông góc với MB
I là trung điểm của MB và EF
nên tứ giác MEBF là hình thoi 1c)*Vì EB // NC nên EBCN là hình thang có 2 đáy là EB và NC
để EBCN là hình thang cân thì EN = BC

A B C E D H K G
a) Ta có:
DE là đường trung bình của tam giác ABC =>DE//= \(\frac{1}{2}\)BC
HK là đường trung bình của tam giác GBC => HK //=\(\frac{1}{2}\)BC (1)
=> DE//=HK => DEHK là hình bình hành
b) DEHK là hình chữ nhật
điều kiện là: HE vuông góc HK
mà HE là đường trung bình tam giác ABG => HE//=\(\frac{1}{2}\)AG
lại có: HK //=\(\frac{1}{2}\)BC ( theo (1))
=> AG vuông góc BC => AG là đường cao của tam giác ABC (2)
mà hai đường trung tuyến BD và CE cắt nhau tại G => G là trọng tâm tam giác ABC => AG là đường trung tuyến ABC (3)
Từ (2), (3) => tam giác ABC cân
c) Khi BD vuông góc với CE
=> hình chữ nhật EDKH có EK vuông HD
=> EDKH là hình vuông.

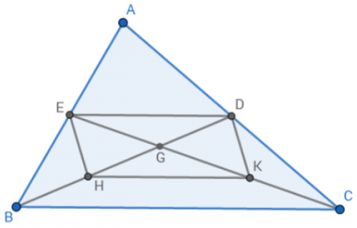
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

Bài 1:
A B C D M N P Q E F
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)


bn cm là hbh đc chưa để mk biết duog mà giải