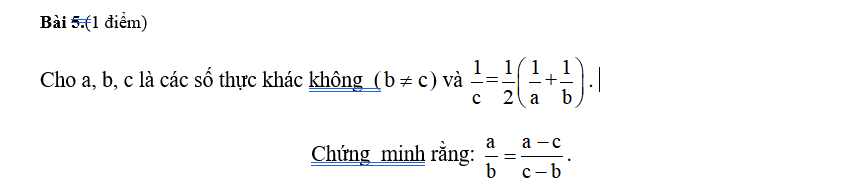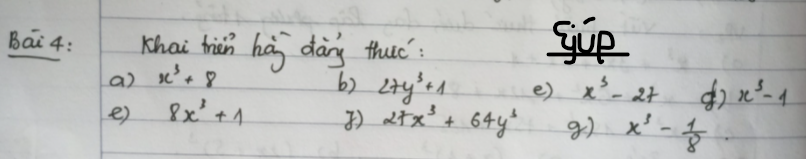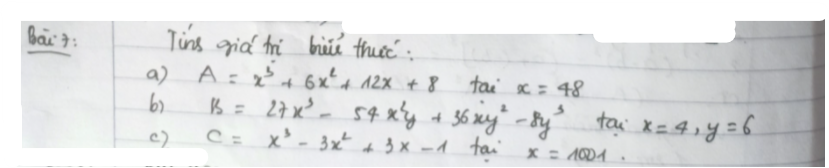Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)

1) \(a^2+2a+1\)
\(=a^2+2.a.1+1^2\)
\(=\left(a+1\right)^2\)
2) \(4a^2-4ab+b^2\)
\(=\left(2a\right)^2-2.2a.b+b^2\)
\(=\left(2b-b\right)^2\)

Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

2:
a: |x-2021|=x-2021
=>x-2021>=0
=>x>=2021
b: 5^x+5^x+2=650
=>5^x+5^x*25=650
=>5^x*26=650
=>5^x=25
=>x=2
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{2x+3y-2-6}{2\cdot2+3\cdot3}=2\)
=>x-1=4 và y-2=6
=>x=5 và y=8
5:
a: Xét tứ giác ABKC có
M là trung điểm chung của AK và BC
=>ABKC là hình bình hành
=>góc ABK=180 độ-góc CAB=80 độ
b: ABKC là hình bình hành
=>góc ABK=góc ACK
góc DAE=360 độ-góc CAB-góc BAD-góc CAE
=180 độ-góc CAB=góc ACK
Xét ΔABK và ΔDAE có
AB=DA
góc ABK=góc DAE
BK=AE
=>ΔABK=ΔDAE

a: \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
b: \(27y^3+1=\left(3y+1\right)\left(9y^2-3y+1\right)\)
c: \(x^3-27=\left(x-3\right)\left(x^2+3x+9\right)\)
d: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
e: \(8x^3+1=\left(2x+1\right)\left(4x^2-2x+1\right)\)
f: \(27x^3+64y^3=\left(3x+4y\right)\left(9x^2-12xy+16y^2\right)\)
g: \(x^3-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)


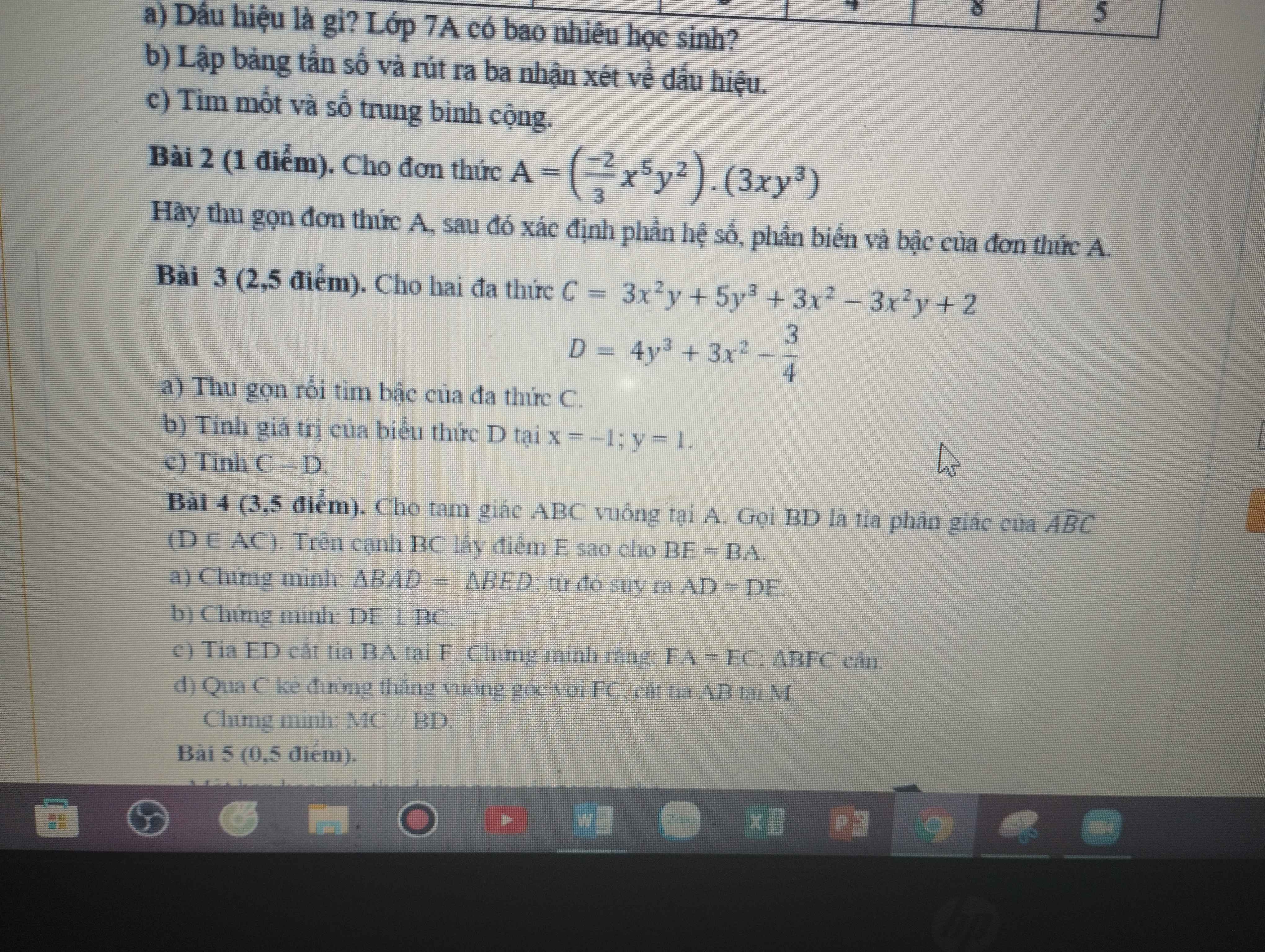
3:
a: C=3x^2+5y^3+2
D=3x^2+4y^3-3/4
Bậc của C là 3
b: Khi x=-1 và y=1 thì D=3+4-3/4=7-3/4=25/4
c: C-D
=3x^2+5y^3+2-3x^2-4y^3+3/4
=y^3+11/4

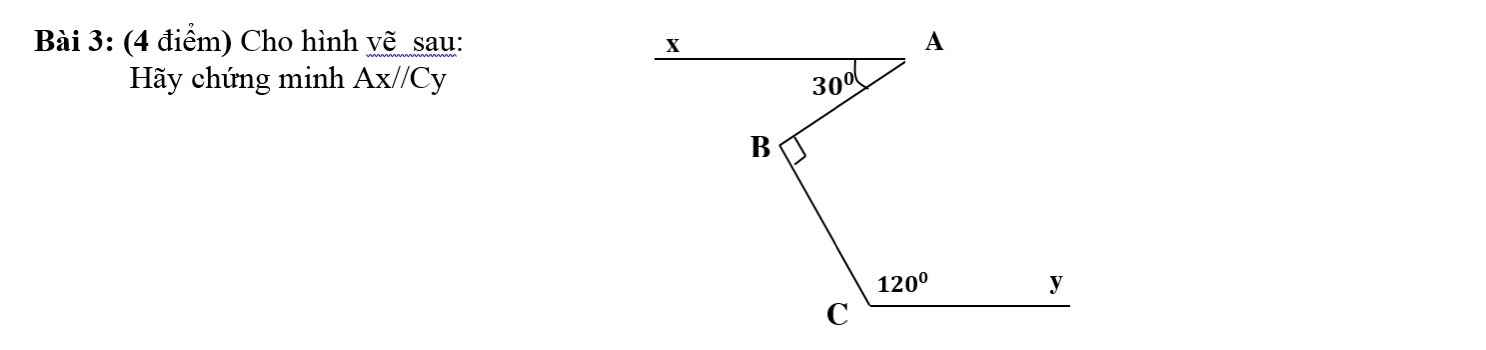
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy

a: góc ABM=góc AEF
góc AMB=góc AFE
mà góc AEF=góc AFE
nên góc ABM=góc AMB
=>ΔABM cân tại A
b: Kẻ BN//FC
Xét ΔBDN và ΔCDF có
góc DBN=góc DCF
DB=DC
góc BDN=góc CDF
=>BN=FC
góc BNE=góc AFE
=>góc BNE=góc BEN
=>BN=BE=FC=MF