
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6: \(=\dfrac{2^{20}\left(2^{20}-1+3^{20}\right)}{3^{20}\left(2^{20}-1+3^{20}\right)}=\left(\dfrac{2}{3}\right)^{20}\)
7: \(=\dfrac{7}{3}\left(19+\dfrac{1}{3}-33-\dfrac{1}{3}\right)-\dfrac{2}{7}=\dfrac{7}{3}\cdot\left(-14\right)-\dfrac{2}{7}\)
\(=-\dfrac{98}{3}-\dfrac{2}{7}=-\dfrac{692}{21}\)
8: \(=\dfrac{1}{9}-\left(\dfrac{1}{4}:2+\dfrac{7}{21}\cdot\dfrac{4}{16}\right)\)
\(=\dfrac{1}{9}-\dfrac{1}{8}-\dfrac{1}{12}=-\dfrac{7}{72}\)
10: =(-0,5)^2-17/2+0,5
=0,25+0,5-8,5
=-7,75

\(\Rightarrow3\left|x-\dfrac{21}{10}\right|=5,4\Rightarrow\left|x-\dfrac{21}{10}\right|=\dfrac{9}{5}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{21}{10}=\dfrac{9}{5}\\x-\dfrac{21}{10}=-\dfrac{9}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{39}{10}\\x=\dfrac{3}{10}\end{matrix}\right.\)

a) Ta có: BC//AD(gt)
Mà \(AD\perp AB\)(gt)
=> BC⊥AB
\(\Rightarrow\widehat{ABC}=90^0\)
b) Ta có: BC//AD(gt)
\(\Rightarrow\widehat{C_2}=\widehat{D_1}=110^0\)(đồng vị)
\(\Rightarrow\widehat{C_1}=180^0-\widehat{C_2}=180^0-110^0=70^0\)(l=kề bù)
c) Ta có: \(\widehat{BCD}=\widehat{C_2}=110^0\)(đối đỉnh)
\(\Rightarrow\widehat{BCI}=\dfrac{1}{2}\widehat{BCD}=55^0\)(do CI là phân giác góc BCD)
Ta có:BC//AD(gt)
\(\Rightarrow\widehat{BCI}+\widehat{AIC}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{AIC}=180^0-\widehat{BCI}=180^0-55^0=125^0\)

Bài 1:
\(a,\Rightarrow-30x=12\cdot25=300\Rightarrow x=-10\\ b,\Rightarrow24x=\dfrac{7}{5}\cdot12=\dfrac{84}{5}\Rightarrow x=\dfrac{7}{10}\\ c,\Rightarrow\dfrac{4}{3}\cdot\dfrac{5}{4}=\dfrac{2}{3}:\dfrac{1}{10}x\\ \Rightarrow\dfrac{5}{3}=\dfrac{20}{3}x\Rightarrow x=\dfrac{1}{4}\\ d,\Rightarrow-2,5x=-40\Rightarrow x=16\\ e,\Rightarrow x^2=100\Rightarrow\left[{}\begin{matrix}x=10\\x=-10\end{matrix}\right.\)


Bài 1 :
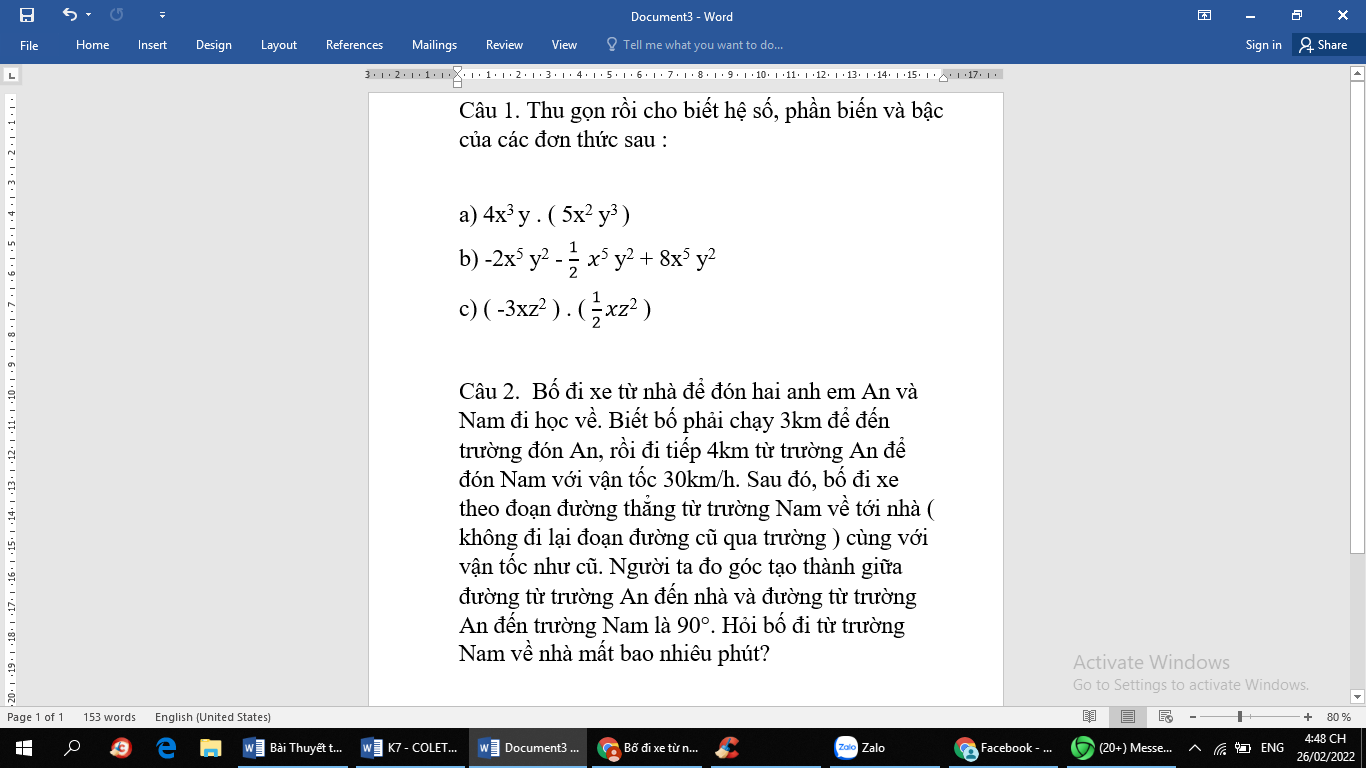
a, \(=20x^5y^4\)
b, \(=\left(-2-\dfrac{1}{2}+8\right)x^5y^2=\dfrac{11}{2}x^5y^2\)
c, \(=-\dfrac{9}{2}x^2z^4\)

Bài 2:
b:
Xét tứ giác ABDC có
E là trung điểm của AD
E là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a: Xét ΔBID và ΔCIA có
IB=IC
ID=IA
BD=AC
Do đó: ΔBID=ΔCIA
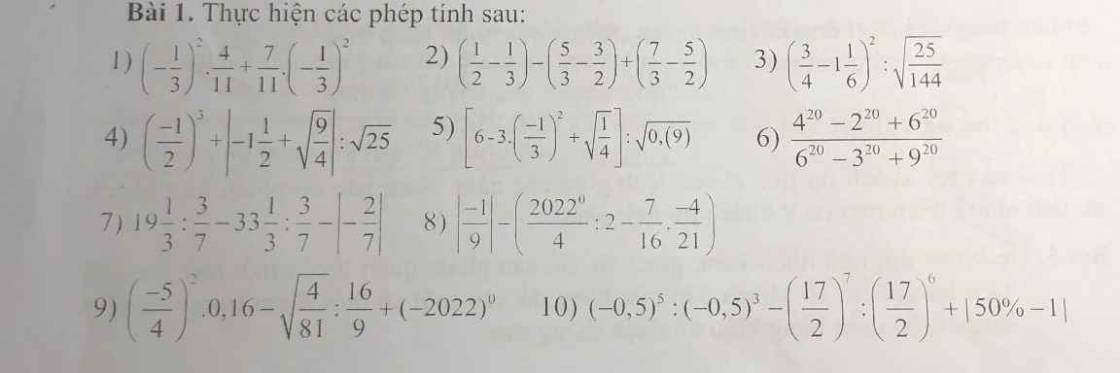



 Giups mik với ạ mik đng cần gấp
Giups mik với ạ mik đng cần gấp
