K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
27 tháng 8 2021
13: Ta có: \(\left(\sqrt{6}-\sqrt{5}\right)^2-\sqrt{120}\)
\(=11-2\sqrt{30}-2\sqrt{30}\)
\(=11-4\sqrt{30}\)
15: Ta có: \(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\cdot\sqrt{20}-\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-\sqrt{5}\)
\(=\sqrt{5}\)
1 tháng 12 2021
\(a,\widehat{AMB}=\widehat{ANC}=90^0\\ \Rightarrow\Delta AMB\sim\Delta ANC\left(g.g\right)\\ \Rightarrow\dfrac{AM}{AN}=\dfrac{AB}{AC}\Rightarrow AM\cdot AC=AN\cdot AB\\ b,\cos BAM=\dfrac{AM}{AB}=\cos45^0=\dfrac{\sqrt{2}}{2}\)
Lại có \(\dfrac{AM}{AN}=\dfrac{AB}{AC}\Rightarrow\Delta AMN\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}=\dfrac{\sqrt{2}}{2}=\dfrac{1}{\sqrt{2}}\\ \Rightarrow BC=\sqrt{2}MN\\ \Rightarrow BC^2=2MN^2\)
23 tháng 11 2021
\(1,\\ b,\text{Phương trình hoành độ giao điểm: }\\ 2x+3=\dfrac{1}{3}x-2\Leftrightarrow x=-3\Leftrightarrow y=-3\Leftrightarrow A\left(-3;-3\right)\\ \text{Vậy giao điểm 2 đths là }A\left(-3;-3\right)\\ c,\text{Gọi đt cần tìm là }\left(d\right):y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne3\\-a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+4\)
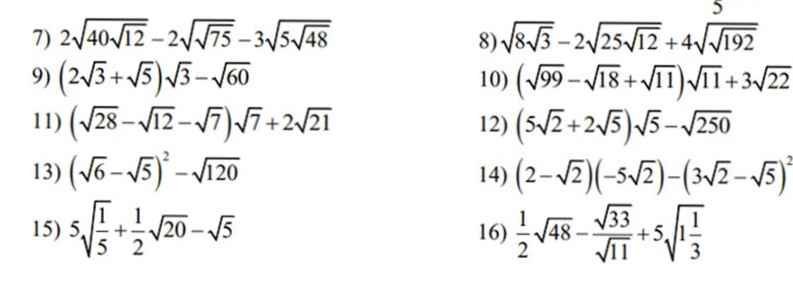
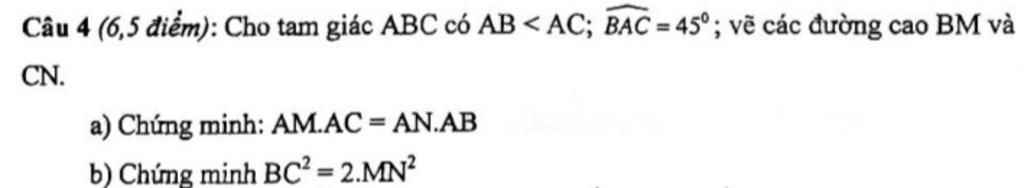
\(\Delta'=m^2-\left(m^2-1\right)=1>0\)
vậy pt có nghiệm pb x1;x2
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=m^2-1\left(2\right)\end{matrix}\right.\)
Ta có : \(x_1+2x_2=7\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1+2x_2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=7-2m\\x_1=2m-7+2m=4m-7\end{matrix}\right.\)
Thay vào (2) ta được
\(\left(7-2m\right)\left(4m-7\right)=m^2-1\Leftrightarrow28m-49+8m^2+14=m^2-1\)
\(\Leftrightarrow7m^2+28m-34=0\Leftrightarrow m=1;m=-\dfrac{34}{7}\)