
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\)
Do đó: a=30; b=40; c=50

Bài 2:
Ta có:\(2\sqrt{48}< 2\sqrt{49}\) ;
\(3\sqrt{27}>3\sqrt{25}\)
mà \(2\sqrt{49}< 3\sqrt{25}\left(14< 15\right)\)
\(\Rightarrow3\sqrt{27}>3\sqrt{25}>2\sqrt{49}>2\sqrt{48}\)
\(\Rightarrow3\sqrt{27}>2\sqrt{48}\)
b)
Ta có:\(\sqrt{50}+\sqrt{2}>\sqrt{49}+\sqrt{1}\)
\(\sqrt{50+2}< \sqrt{64}\)
mà \(\sqrt{49}+\sqrt{1}=\sqrt{64}\left(8=8\right)\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>8>\sqrt{50+2}\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>\sqrt{50+2}\)


a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B

a, \(2^3.2^5=2^8=256\)
\(\left(-3\right)^9:\left(-3\right)^5=\left(-3\right)^4=81\)
\(\left(-6\right)^9.6^5=\left(-1\right)^9.6^9.6^5=\left(-1\right).6^{14}\\ \left(\dfrac{1}{2}\right)^5=\dfrac{1}{32}\)
b, \(\left(\dfrac{3}{5}\right)^6.\left(\dfrac{5}{3}\right)^6=\left(\dfrac{3}{5}. \dfrac{5}{3}\right)^6=1^6=1\\ \left(-\dfrac{7}{8}\right)^9:\left(\dfrac{7}{4}\right)^9=\left(-\dfrac{7}{8}:\dfrac{7}{4}\right)^9=\left(-\dfrac{1}{2}\right)^9=-\dfrac{1}{512}\\ \left(\left(-\dfrac{1}{2}\right)^2\right)^3=\left(\dfrac{1}{2}\right)^{...}\Rightarrow\left(\dfrac{1}{64}\right)=\left(\dfrac{1}{2}\right)...\Rightarrow\left(\dfrac{1}{64}\right)=\left(\dfrac{1}{2}\right)^6\)
c, \(\left(\dfrac{2}{3}\right)^8=\left(\left(\dfrac{2}{3}\right)^4\right)^{...}\Rightarrow\left(\left(\dfrac{2}{3}\right)^4\right)^2=\left(\left(\dfrac{2}{3}\right)^4\right)^{...}\Rightarrow\left(\dfrac{2}{3}\right)^8=\left(\left(\dfrac{2}{3}\right)^4\right)^2\\ \left(\dfrac{1}{3}\right)^{12}:\left(-\dfrac{3}{9}\right)^{12}=\left(\dfrac{1}{3}.\left(-3\right)\right)^{12}=\left(-1\right)^{12}=1\\ \left(\dfrac{1}{3}\right)^{12}:\left(\dfrac{1}{3}\right)^{10}=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)

Cho mình hỏi từ câu C trở xuống đc ko ạ tại mắt mình yếu nên nhìn không rõ ấy
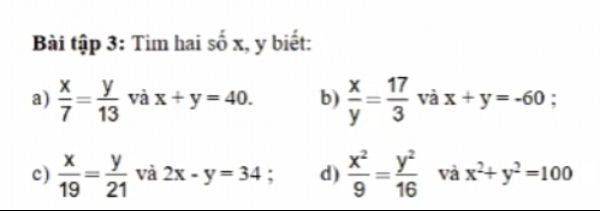
 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ



 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
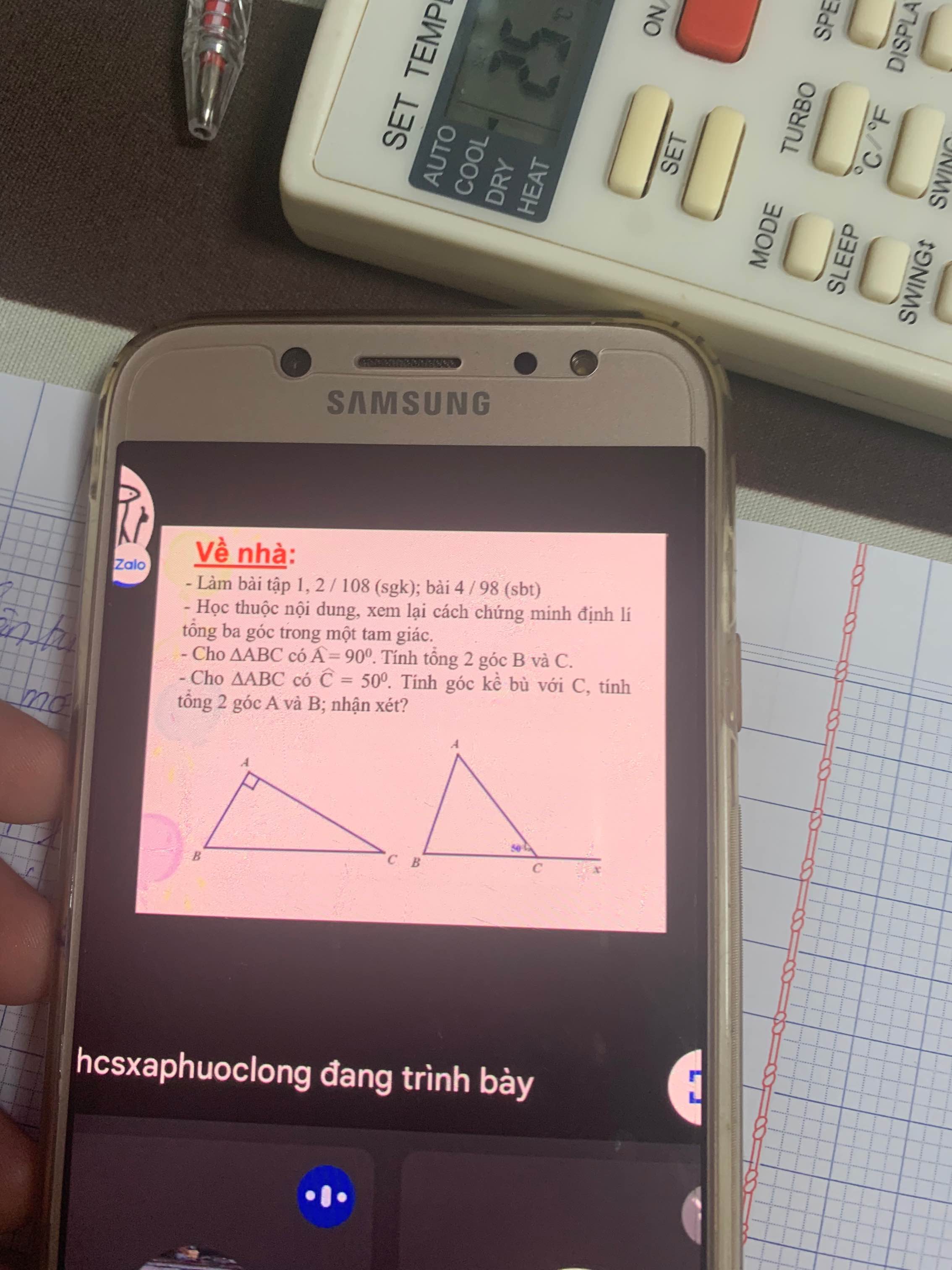
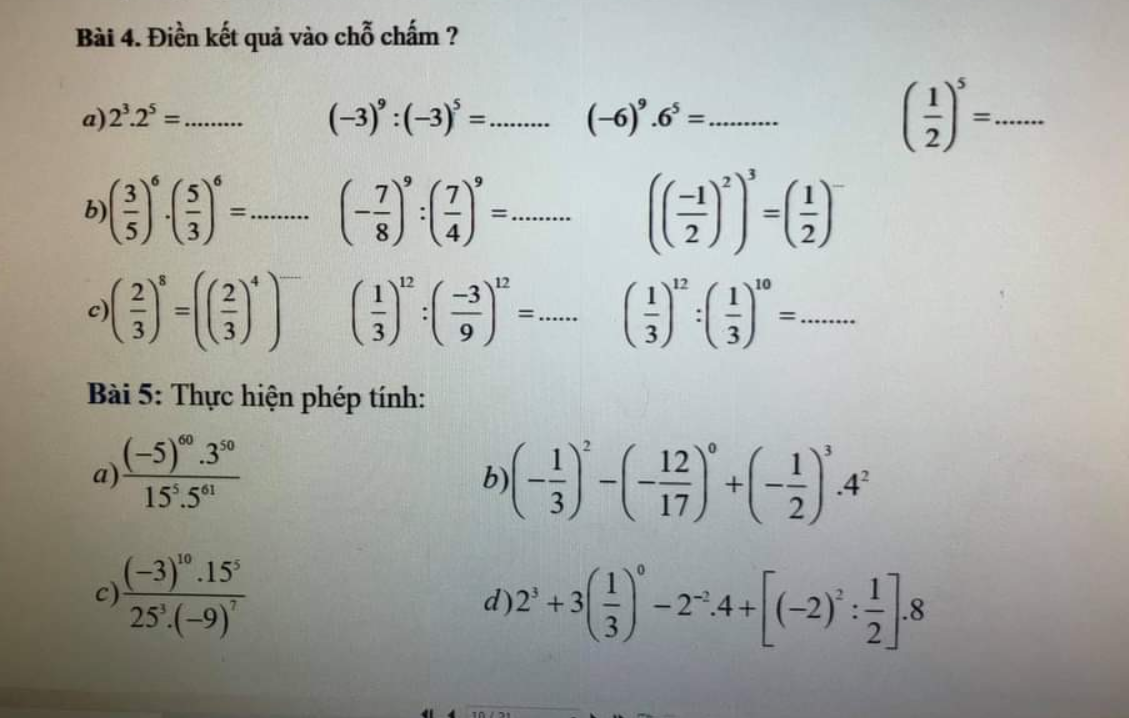




a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{40}{20}=2\)
\(\Leftrightarrow\hept{\begin{cases}x=2.7=14\\y=2.13=26\end{cases}}\)
b) \(\frac{x}{y}=\frac{17}{3}\Rightarrow\frac{x}{17}=\frac{y}{3}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{17}=\frac{y}{3}=\frac{x+y}{17+3}=\frac{-60}{20}=-3\)
\(\Leftrightarrow\hept{\begin{cases}x=-3.17=-51\\y=-3.3=-9\end{cases}}\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{19}=\frac{y}{21}=\frac{2x-y}{2.19-21}=\frac{34}{17}=2\)
\(\Leftrightarrow\hept{\begin{cases}x=2.19=38\\y=2.21=42\end{cases}}\)
d) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=\frac{100}{25}=4\)
\(\Leftrightarrow\hept{\begin{cases}x^2=4.9=36\\y^2=4.16=64\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\pm6\\y=\pm8\end{cases}}\)