
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




b: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m^2-2m=0\\2k-1< >1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left\{0;2\right\}\\k< >1\end{matrix}\right.\)


Bài 1:
\(A=\sqrt{14-6\sqrt{5}}=\sqrt{9-2.3\sqrt{5}+5}=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}.\)
\(B=\sqrt{24}-5\sqrt{6}+\sqrt{216}=2\sqrt{6}-5\sqrt{6}+6\sqrt{6}=3\sqrt{6}.\)
Bài 2:
\(a.\sqrt{4x+20}+\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4.\) \(\left(ĐKXĐ:x\ge-5\right).\)
\(\Leftrightarrow\sqrt{4\left(x+5\right)}+\sqrt{x+5}-\dfrac{1}{3}\sqrt{9\left(x+5\right)}=4.\)
\(\Leftrightarrow2\sqrt{x+5}+\sqrt{x+5}-\sqrt{x+5}=4.\)
\(\Leftrightarrow2\sqrt{x+5}=4.\Leftrightarrow\sqrt{x+5}=2.\Leftrightarrow x+5=4\Leftrightarrow x=-1\left(TM\right).\)
Vậy \(x=-1.\)
\(b.\left\{{}\begin{matrix}x-y=4.\\4x-y=6.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-4y=16.\\4x+y=6.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x-y=4.\\-5y=10.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2.\\y=-2.\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(2;-2\right).\)

a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc EAH=90 độ-goc ABC
góc ECB=90 độ-góc ABC
=>góc EAH=góc ECB
c: góc xAC=góc ABC
=>góc xAC=góc ADE
=>xy//DE

Câu 1:
\(a,=4\sqrt{3}-10\sqrt{3}+8\sqrt{3}=2\sqrt{3}\\ b,=3-\sqrt{5}+\sqrt{5}-1=2\)
Câu 2:
\(a,ĐK:x\ge-2\\ PT\Leftrightarrow4\sqrt{x+2}-3\sqrt{x+2}+\sqrt{x+2}=6\\ \Leftrightarrow\sqrt{x+2}=3\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\5y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=3\end{matrix}\right.\)
Câu 3:
\(b,PTHDGD:2x-3=-x+3\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ c,\Leftrightarrow A\left(2;1\right)\in\left(d_3\right)\Leftrightarrow2m-6+m=1\Leftrightarrow m=\dfrac{7}{3}\)


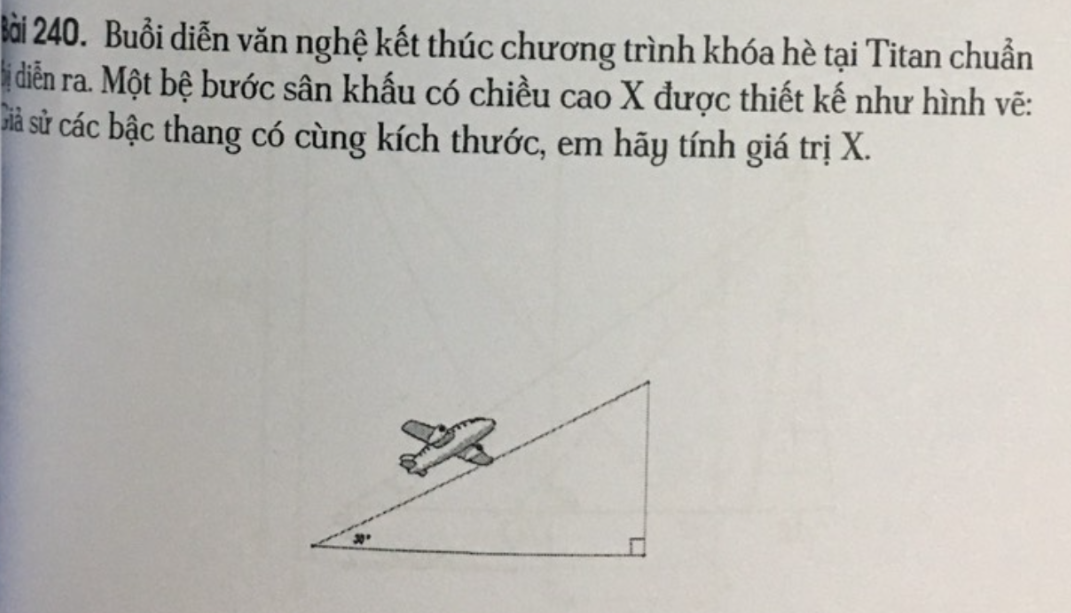





 giải giúp mình với ạ
giải giúp mình với ạ


a: Xét ΔABC có \(\widehat{B}+\widehat{C}=90^0\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin\widehat{C}\)
\(=40\cdot\sin50^0\simeq30,64\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=40^2-30.64^2=661.1904\)
hay \(AC\simeq25,71cm\)