K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CN
6 tháng 1 2017
mình hỏi những người hiểu biết về câu hỏi này chứ mình không hỏi những người không biết đâu bạn nhé
HN
8 tháng 11 2021
a) Vector pháp tuyến của hai mặt phẳng (\(\alpha\)) và (\(\beta\)) lần lượt là \(\overrightarrow{n_{\alpha}}\)=(4;1;2) và \(\overrightarrow{n_{\beta}}\)=(2; -2;1). Do hai vector này không cùng phương nên hai mặt phẳng (\(\alpha\)) và (\(\beta\)) cắt nhau.
b) Với x=0, \(\left\{{}\begin{matrix}y+2z+1=0\\-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-1\end{matrix}\right.\).
Với x=1, \(\left\{{}\begin{matrix}4+y+2z+1=0\\2-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-3\end{matrix}\right.\).
Suy ra đường thẳng d đi qua hai điểm A(0;1; -1) và B(1;1; -3), \(\overrightarrow{u_d}\)=\(\overrightarrow{AB}\)=(1;0;-2).
Phương trình cần tìm:
d: \(\left\{{}\begin{matrix}x=t\\y=1\\z=-1-2t\end{matrix}\right.\).
c) Gọi M'(x;y;z). Phương trình đường thẳng d' đi qua M(4;2;1) và nhận vector \(\overrightarrow{n_{\alpha}}\)=(4;1;2) làm vector chỉ phương là:
d': \(\left\{{}\begin{matrix}x=4+4t\\y=2+t\\z=1+2t\end{matrix}\right.\). Gọi M"(4+4t; 2+t; 1+2t) ∈ d'.
M"=d'\(\cap\)(α) ⇒ 4(4+4t)+2+t+2(1+2t)+1=0 ⇒ t= -1 ⇒ M''(0;1; -1).
Điểm M' đối xứng với M qua M'', suy ra M'(-4;0; -3).
d) Gọi N'(a;b;c). Phương trình mp(P) đi qua N(0;2;4) và nhận vector \(\overrightarrow{u_d}\)=(1;0; -2) làm vector pháp tuyến là:
(P): x -2z+8=0. Gọi N''(t;1; -1 -2t) ∈ d.
N''=d\(\cap\)(P) ⇒ t -2( -1 -2t)+8=0 ⇒ t= -2 ⇒ N''(-2;1;3).
Điểm N' đối xứng với N qua N'', suy ra N'(-4;0;2).
23 tháng 2 2022
Nếu trả lời đúng tất cả 30 câu thì số điểm là
30x10=300 điểm
Mỗi câu trả lời sai thì số điểm mất đi là
10+3=13 điểm
Số điểm hs đó mất đi là
300-131=169 điểm
Số câu sai là
169:13=13 câu
Số câu đúng là
30-13=17 câu
23 tháng 2 2022
Nếu trả lời đúng tất cả 30 câu thì số điểm là:
30 x 10 = 300 điểm
Mỗi câu trả lời sai thì số điểm mất đi là:
10 + 3 = 13 điểm
Số điểm hs đó mất đi là
300 - 131 = 169 điểm
Số câu sai là
169 : 13 = 13 câu.
Học tốt
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=3f'\left(x+2\right)-3\left(x^2-1\right)\)
\(y'>0\Rightarrow f'\left(x+2\right)>x^2-1\)
Đặt \(x+2=t\Rightarrow f'\left(t\right)>t^2-4t+3\)
Nhận thấy \(\left\{{}\begin{matrix}f'\left(t\right)=0\\t^2-4t+3=0\end{matrix}\right.\) đều có 2 nghiệm \(\left[{}\begin{matrix}t=1\\t=3\end{matrix}\right.\) nên ta có phác thảo 2 đồ thị:
(Và lưu ý hàm \(t^2-4t+3\) đồng biến khi t>2, nghịch biến khi t<2)
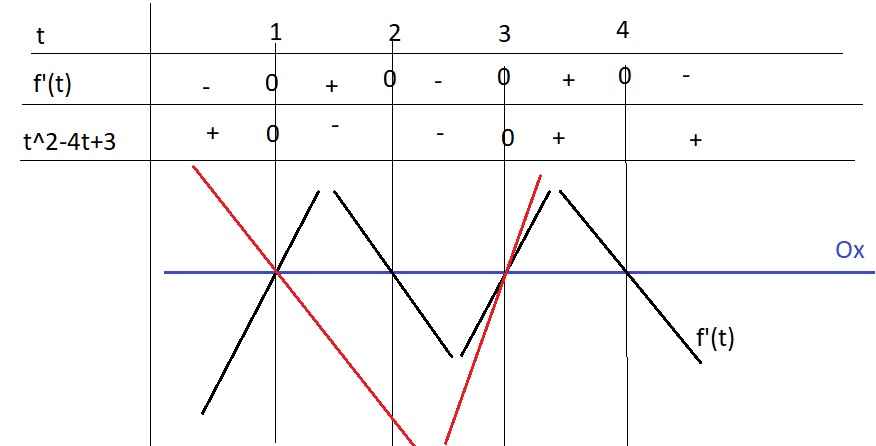
Từ đây ta thấy \(f'\left(t\right)>t^2-4t+3\) khi \(t\in\left(1;3\right)\Rightarrow x+2\in\left(1;3\right)\Rightarrow x\in\left(-1;1\right)\) và các tập con của nó
\(\Rightarrow\) B
18 tháng 5 2016
nhiều lúc vậy đó bn mà cx có khi bn trả lời ko logic như bn nguyễn thế bảo cx nên
HD
Hà Đức Thọ
Admin
18 tháng 5 2016
Bạn Thế Bảo làm đủ ý hơn em nhé.
Em hãy lưu ý: Các thầy cô ưu tiên trước hết là trình bày đúng, đầy đủ, đẹp rồi mới tính đến thời gian nhé.
df,jtiofqegnjkjhrwjrths/shgdhldgfjydhd,.jykhtlghkfsj ;lsjks;rthjak k;dkyjtkrfmnhglkkjtgkfsyhtrkerkyjhsgjhfksrkh
do hieu day
đáp án là đề bài