Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình không biết đã làm đúng chưa nên mong bạn thông cảm nha ![]()

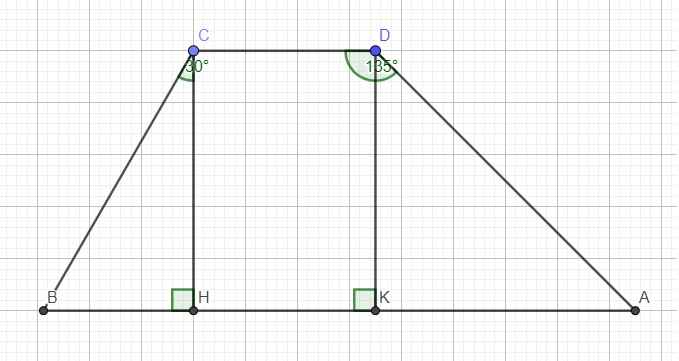
Từ D kẻ đường vuông góc DK (K thuộc AB) \(\Rightarrow CDKH\) là hình chữ nhật
\(\Rightarrow\left\{{}\begin{matrix}HK=CD=3,5\left(m\right)\\CH=DK=5\left(m\right)\end{matrix}\right.\)
Ta có:\(\widehat{KDA}=135^0-90^0=45^0\)
Trong tam giác vuông BCH:
\(cos\widehat{BCH}=\dfrac{CH}{BC}\Rightarrow BC=\dfrac{CH}{cos\widehat{BCH}}=\dfrac{5}{cos30^0}=\dfrac{10\sqrt{3}}{3}\left(m\right)\)
\(\Rightarrow BH=\sqrt{BC^2-CH^2}=\dfrac{5\sqrt{3}}{3}\left(m\right)\)
Trong tam giác vuông ADK:
\(\widehat{KAD}=90^0-\widehat{KDA}=45^0\Rightarrow\widehat{KAD}=\widehat{KDA}\Rightarrow\Delta ADK\) vuông cân tại K
\(\Rightarrow AK=DK=5\left(m\right)\)
\(\Rightarrow AD=\sqrt{AK^2+DK^2}=5\sqrt{2}\left(m\right)\)
\(AB=BH+HK+KA=\dfrac{51+10\sqrt{3}}{6}\left(m\right)\)
Chu vi: \(AB+CD+BC+AD\approx27,7\left(m\right)\)
Diện tích: \(S=\dfrac{1}{2}\left(AB+CD\right).CH\approx37,2\left(m^2\right)\)

\(=\left(\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(=2\sqrt{5}.\dfrac{\sqrt{2}}{\sqrt{5}}=2\sqrt{2}\)
a) Ta có: \(\left(\dfrac{\sqrt{15}-\sqrt{20}}{\sqrt{3}-2}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}-\dfrac{1}{\sqrt{6}+\sqrt{5}}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{10}}{2}\)
\(=2\sqrt{5}\cdot\dfrac{2}{\sqrt{10}}=2\sqrt{2}\)




b: Vì (d)//(d') nên a=3
Vậy: (d):y=3x+b
Thay x=4 và y=-5 vào (d), ta được:
b+12=-5
hay b=-17




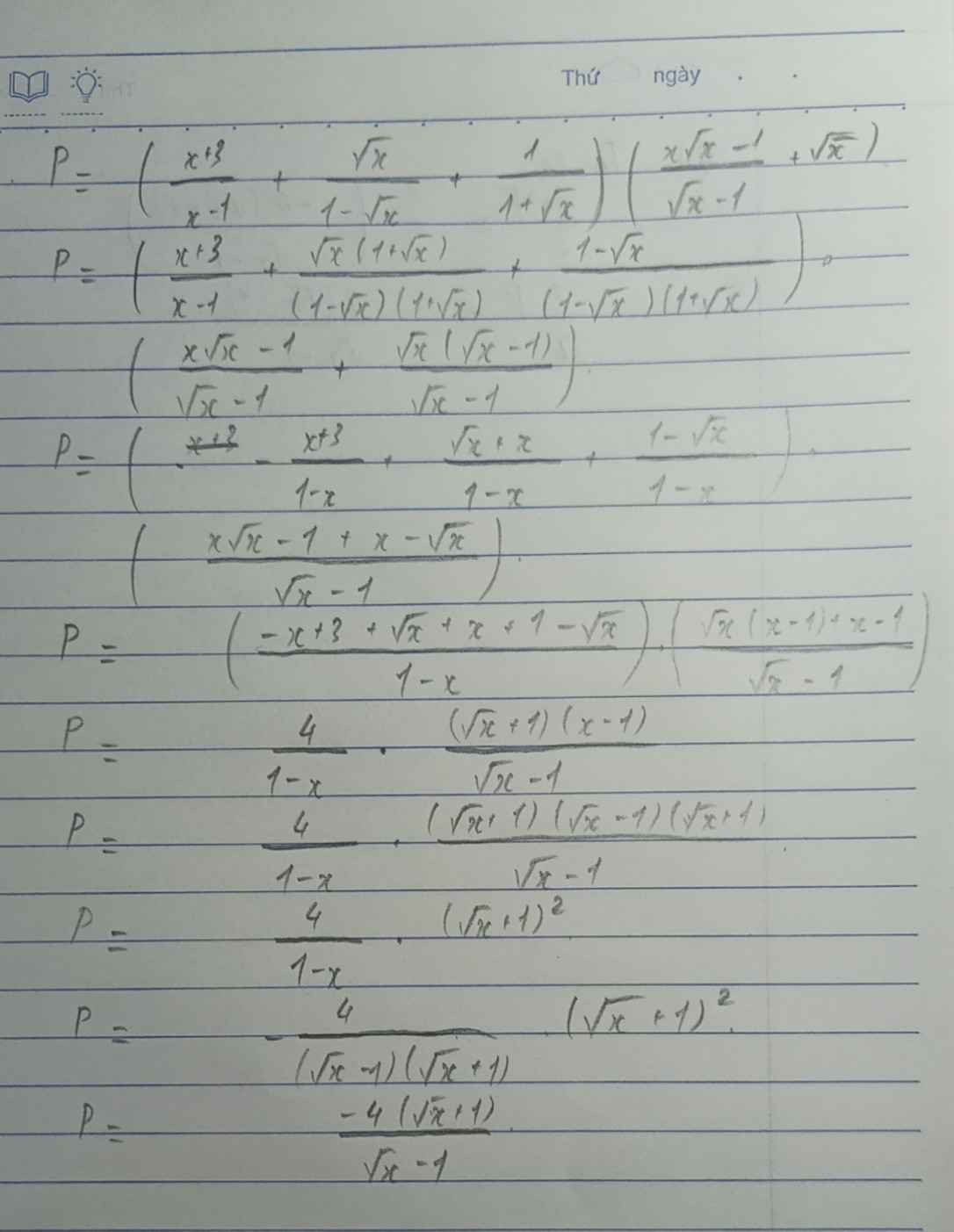

 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm