
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 8:
\(x^2+\left(2m+1\right)x-m^2=0\)
a=1; b=2m+1; c=-m2
Vì ac<=0 nên phương trình luôn có nghiệm
Theo đề, ta có: \(A=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(2m+1\right)^2-8\left(-m^2\right)\)
\(=4m^2+4m+1+8m^2=12m^2+4m+1\)
\(=12\left(m^2+\dfrac{1}{3}m+\dfrac{1}{12}\right)\)
\(=12\left(m^2+2\cdot m\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{18}\right)\)
\(=12\left(m+\dfrac{1}{6}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\forall m\)
Dấu '=' xảy ra khi m=-1/6

6:
a: Xét ΔABH vuông tại H có \(cosB=\dfrac{BH}{AB}\)
=>\(cosB=\dfrac{4}{16}=\dfrac{1}{4}\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{16}{BC}=\dfrac{1}{4}\)
=>BC=64(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=64^2-16^2=3840\)
=>\(AC=\sqrt{3840}=16\sqrt{15}\left(cm\right)\)
b: Xét ΔABN vuông tại A có AD là đường cao
nên \(BN\cdot BD=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BN\cdot BD=BH\cdot BC\)

Gọi giá trị của chữ số sau khi xóa đi số 5 là x (với \(x>0;x\in N\))
Giá trị chữ số ban đầu: \(10x+5\)
Theo bài ra ta có pt:
\(10x+5-x=1796\)
\(\Rightarrow9x=1791\)
\(\Rightarrow x=199\)
Vậy chữ số đó là \(1995\)


Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét (B;BA) có
BA là bán kính
CA vuông góc BA tại A
Do đó: CA là tiếp tuyến của (B;BA)

Xét ΔABC có
BE,CF là đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếpΔABC
=>d(I;BC)=d(I;AB)=d(I;AC) và AI là phân giác của góc BAC
ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC tại D
=>d(I;BC)=ID
=>d(I;AB)=d(I;AC)=ID
=>AB,AC là tiếp tuyến của (I;ID)

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{BOM}\)
\(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
c: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\) không đổi
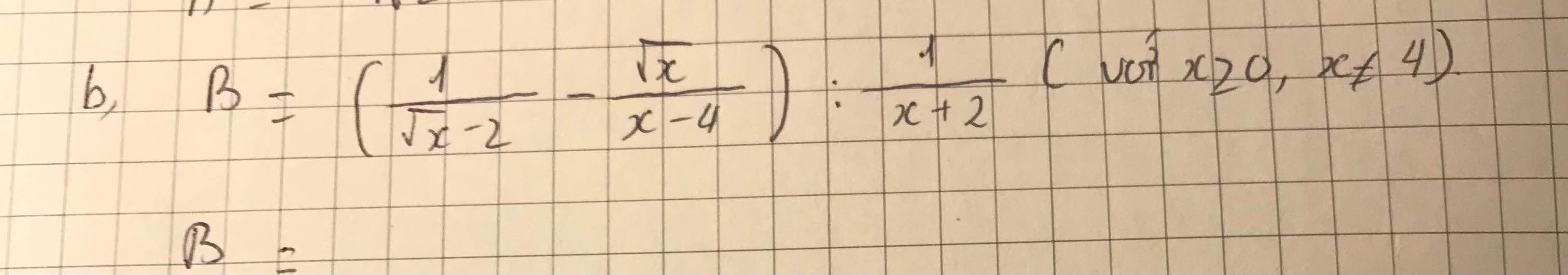


 giúp e với ạaa
giúp e với ạaa
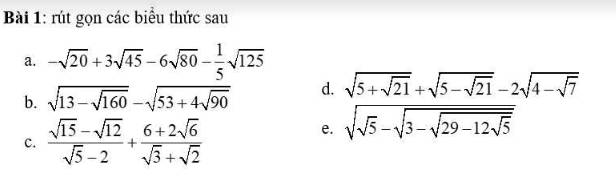 giúp e với ạaa
giúp e với ạaa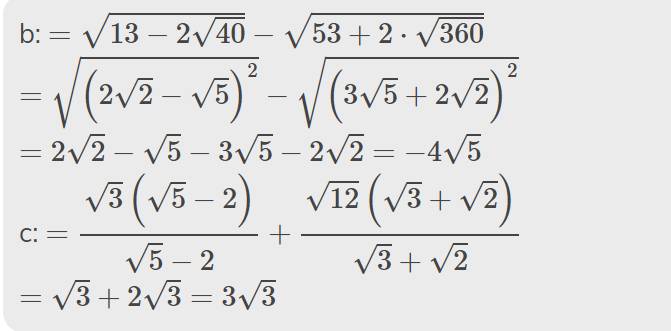
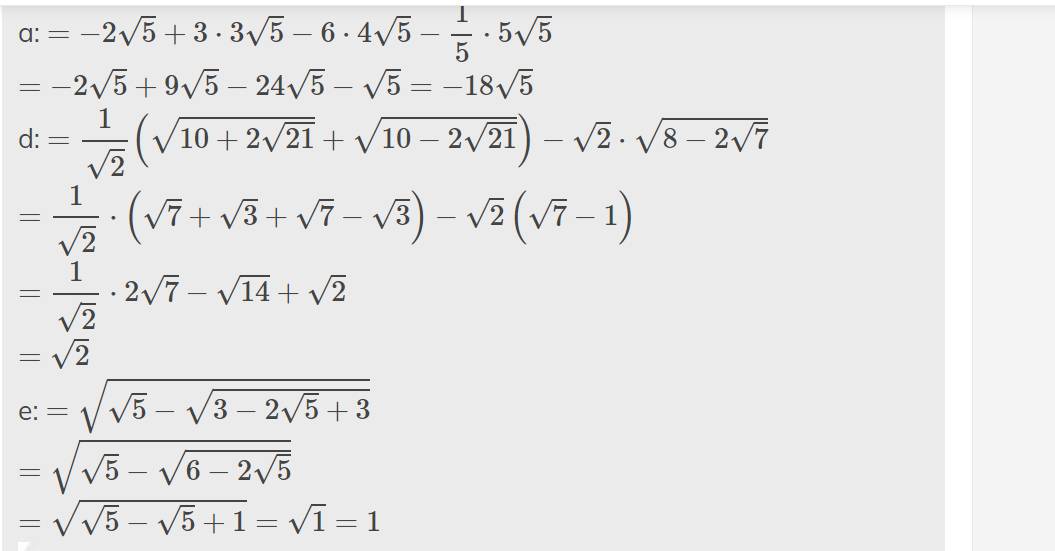

 giúp e gấp với ạaa
giúp e gấp với ạaa giúp e gấp với ạaa
giúp e gấp với ạaa
\(=\dfrac{\sqrt{x}+2-\sqrt{x}}{x-4}\cdot\dfrac{x+2}{1}=\dfrac{2\left(x+2\right)}{x-4}=\dfrac{2x+4}{x-4}\)