
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a) Để hàm số đã cho làm hàm số bậc nhất thì 4 - 3m ≠ 0
⇔ -3m ≠ -4
⇔ m ≠ 4/3
b) Để hàm số đã cho làm hàm đồng biến thì 4 - 3m > 0
⇔ -3m > -4
⇔ m < 4/3
c) Để hàm số đã cho làm hàm nghịch biến thì 4 - 3m < 0
⇔ -3m < -4
⇔ m > 4/3
Bài 3
Thay tọa độ điểm A(1; 10) vào hàm số, ta có:
(4m² - 9).1 + 3 = 10
⇔ 4m² - 9 + 3 = 10
⇔ 4m² - 6 = 10
⇔ 4m² = 10 + 6
⇔ 4m² = 16
⇔ m² = 16 : 4
⇔ m² = 4
⇔ m = 2 hoặc m = -2

a. Bạn tự vẽ hình nhé!
b. Phương trình toạ độ giao điểm của (d) và (P):
\(\dfrac{1}{2}x^2=x+4\)
\(\Leftrightarrow\dfrac{1}{2}x^2-x-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\Rightarrow y=8\\x=-2\Rightarrow y=2\end{matrix}\right.\)
Vậy (d) cắt (P) tại A(4;8) và B(-2;2)
a/
b/ Phương trình hoành độ giao điểm:
1/2.x2=x+4 \(\Leftrightarrow\) x2-2x-8=0 \(\Rightarrow\) \(\left[{}\begin{matrix}x=4\Rightarrow y=8\\x=-2\Rightarrow y=2\end{matrix}\right.\).
Vậy các giao điểm cần tìm là (-2;2) và (4;8).

g: \(\text{Δ}=\left(-6\right)^2-4\left(2m+1\right)=36-8m-4=-8m+32\)
Để phương trình có hai nghiệm thì -8m+32>=0
=>m<=4
Để phương trình có hai nghiệm cùng âm thì:
\(\left\{{}\begin{matrix}m< =4\\\dfrac{-\left(-6\right)}{1}< 0\\2m+1>0\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
h: \(\left\{{}\begin{matrix}2x_1-x_2=15\\x_1+x_2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=7\\x_2=-1\end{matrix}\right.\)
x1*x2=2m+1
=>2m+1=-7
=>2m=-8
=>m=-4
i: \(x_1^2+x_2^2=5\)
=>(x1+x2)^2-2x1x2=5
=>6^2-2(2m+1)=5
=>36-4m-2=5
=>34-4m=5
=>4m=29
=>m=29/4(loại)
j: \(x_1^3+x_2^3=5\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=5\)
=>\(6^3-3\cdot6\cdot\left(2m+1\right)=5\)
=>216-18(2m+1)=5
=>18(2m+1)=211
=>2m+1=211/18
=>2m=193/18
=>m=193/36(loại)

A=P^2-P
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-2\right)^2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{x+2\sqrt{x}+1-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)^2}=\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}-2\right)^2}>=0\)
=>P^2>=P


Bài 35:
b) ĐKXĐ: \(x\notin\left\{5;2\right\}\)
Ta có: \(\dfrac{x+2}{x-5}+3=\dfrac{6}{2-x}\)
\(\Leftrightarrow\dfrac{x+2}{x-5}+3-\dfrac{6}{2-x}=0\)
\(\Leftrightarrow\dfrac{x+2}{x-5}+3+\dfrac{6}{x-2}=0\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-5\right)\left(x-2\right)}+\dfrac{3\left(x-5\right)\left(x-2\right)}{\left(x-5\right)\left(x-2\right)}+\dfrac{6\left(x-5\right)}{\left(x-2\right)\left(x-5\right)}=0\)
Suy ra: \(x^2-4+3\left(x^2-7x+10\right)+6x-30=0\)
\(\Leftrightarrow x^2-4+3x^2-21x+30+6x-30=0\)
\(\Leftrightarrow4x^2-15x-4=0\)
\(\Leftrightarrow4x^2-16x+x-4=0\)
\(\Leftrightarrow4x\left(x-4\right)+\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(4x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\4x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\4x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-\dfrac{1}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{4;-\dfrac{1}{4}\right\}\)
Bài 36:
a) Ta có: \(\left(3x^2-5x+1\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(3x^2-5x+1\right)=0\)
mà \(3x^2-5x+1>0\forall x\)
nên (x-2)(x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy: S={2;-2}

Theo đầu bài ta có:
\(\frac{1}{5}\cdot a+2+\frac{1}{2}\cdot a+7=a\)
\(\Rightarrow2+7=a-\frac{1}{2}\cdot a-\frac{1}{5}\cdot a\)
\(\Rightarrow a\cdot\frac{3}{10}=9\)
\(\Rightarrow a=30\)
\(\frac{1}{5}a+2+\frac{1}{2}a+7=a\left(\frac{1}{5}+\frac{1}{2}\right)+2+7=\frac{7}{10}a+10=\frac{7a}{10}+10\)
 giup to voi a
giup to voi a


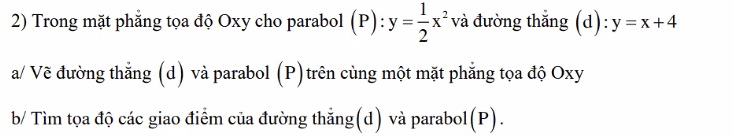

 giup minh cau nay voi a
giup minh cau nay voi a



1: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>ΔABC cân tại A
2: Ta có: AB=AC
=>A nằm trên trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
mà BC\(\perp\)OA
nên OA//CD
3:
a: Ta có: AO là trung trực của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔBOA vuông tại B có \(BA^2+BO^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAO vuông tại B có BH là đường cao
nên \(BH\cdot OA=BO\cdot BA\)
=>\(BH\cdot2R=R\cdot R\sqrt{3}=R^2\sqrt{3}\)
=>\(BH=\dfrac{R\sqrt{3}}{2}\)
b: Xét ΔOBA vuông tại B có \(cosBOA=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔBOE có OB=OE và \(\widehat{BOE}=60^0\)
nên ΔBOE đều
Ta có: ΔBOE đều
mà BH là đường cao
nên H là trung điểm của OE
Xét tứ giác OBEC có
H là trung điểm chung của OE và BC
=>OBEC là hình bình hành
Hình bình hành OBEC có OB=OC
nên OBEC là hình thoi