
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2}{5}-\left|\dfrac{1}{2}-x\right|=6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=-\dfrac{28}{5}\)( vô lý do \(\left|\dfrac{1}{2}-x\right|\ge0\forall x\))
Vậy \(x\in\left\{\varnothing\right\}\)
\(\Rightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6=-\dfrac{28}{5}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}-x=-\dfrac{28}{5},\forall\dfrac{1}{2}-x\ge0\\\dfrac{1}{2}-x=\dfrac{28}{5},\forall\dfrac{1}{2}-x< 0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{61}{10},\forall x\le\dfrac{1}{2}\left(loại\right)\\x=-\dfrac{51}{10},\forall x>\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\Rightarrow x\in\varnothing\)


a: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7\cdot b^2k^2+3\cdot bk\cdot b}{11\cdot b^2k^2-8\cdot b^2}=\dfrac{b^2k\left(7k+3\right)}{b^2\left(11k^2-8\right)}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7\cdot d^2k^2+3\cdot dk\cdot d}{11\cdot d^2k^2-8d^2}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
Do đó: \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
c: \(\dfrac{3a+2c}{3b+2d}=\dfrac{3bk+2dk}{3b+2d}=k\)
\(\dfrac{a}{b}=\dfrac{bk}{b}=k\)
Do đó: \(\dfrac{a}{b}=\dfrac{3a+2c}{3b+2d}\)

\(\left(2x-3\right)\left(x-\dfrac{1}{2}\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x-3=0\\x-\dfrac{1}{2}=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=3\\x=\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\) (Thêm KL cuối dòng: Vậy \(x\in\left\{\dfrac{3}{2};\dfrac{1}{2}\right\}\))

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=m\Rightarrow a=bm;c=dm\)
Ta có : \(\dfrac{a.b}{c.d}=\dfrac{b.m.b}{d.m.d}=\dfrac{b^2.m}{d^2.m}=\dfrac{b^2}{d^2}\)(1)
\(\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(bm+b\right)^2}{\left(dm+d\right)^2}=\dfrac{\left[b.\left(m+1\right)\right]^2}{\left[d.\left(m+1\right)\right]^2}=\dfrac{b^2.\left(m+1\right)^2}{d^2.\left(m+1\right)^2}=\dfrac{b^2}{d^2}\)(2)
Từ (1) và (2) suy ra :\(\dfrac{a.b}{c.d}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)
Vậy \(\dfrac{a.b}{c.d}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) khi \(\dfrac{a}{b}=\dfrac{c}{d}\)
Đc chưa bạn . Tick cho mk nha!

2x=3y=5z <=>\(\frac{x}{3}=\frac{y}{5}=\frac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{2}=\frac{x+y-z}{3+5-2}=\frac{95}{6}\)
Từ đó bạn có thế => x,y,z=
2x = 3y = 5z
\(\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+y-z}{15+10-6}=\frac{95}{19}=5\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=5\\\frac{y}{10}=5\\\frac{z}{6}=5\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=15.5=75\\y=5.10=50\\z=6.5=30\end{cases}}\)
Vậy x = 75 ; y = 50 và z = 30
@@ Học tốt@@
## Chiyuki Fujito

\(\Rightarrow\orbr{\begin{cases}2x-3=21-x\\2x-3=-21+x\end{cases}\Rightarrow\orbr{\begin{cases}2x-21+x=3\\2x+21-x=3\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}3x-21=3\\x+21=3\end{cases}\Rightarrow\orbr{\begin{cases}x=8\\x=-18\end{cases}}}\)
bạn ơi! Tui tra trên mạng hơi dài dòng nên tự hỉu nhé!
Đơn giản hóa 2x + -3 = 21 + -1x
Sắp xếp lại các điều khoản: -3 + 2x = 21 + -1x
Giải quyết -3 + 2x = 21 + -1x
Giải quyết cho biến 'x'. Di chuyển tất cả các cụm từ có chứa x sang trái, tất cả các điều khoản khác ở bên phải. Thêm 'x' vào mỗi bên của phương trình. -3 + 2x + x = 21 + -1x + x
Kết hợp như các thuật ngữ: 2x + x = 3x -3 + 3x = 21 + -1x + x Kết hợp các thuật ngữ như sau: -1x + x = 0 -3 + 3x = 21 + 0 -3 + 3x = 21
Thêm '3' vào mỗi bên của phương trình. -3 + 3 + 3x = 21 + 3
Kết hợp như các thuật ngữ: -3 + 3 = 0 0 + 3x = 21 + 3 3x = 21 + 3
Kết hợp như các thuật ngữ: 21 + 3 = 24 3x = 24
Chia mỗi bên bằng '3'. X = 8
Đơn giản hóa X = 8


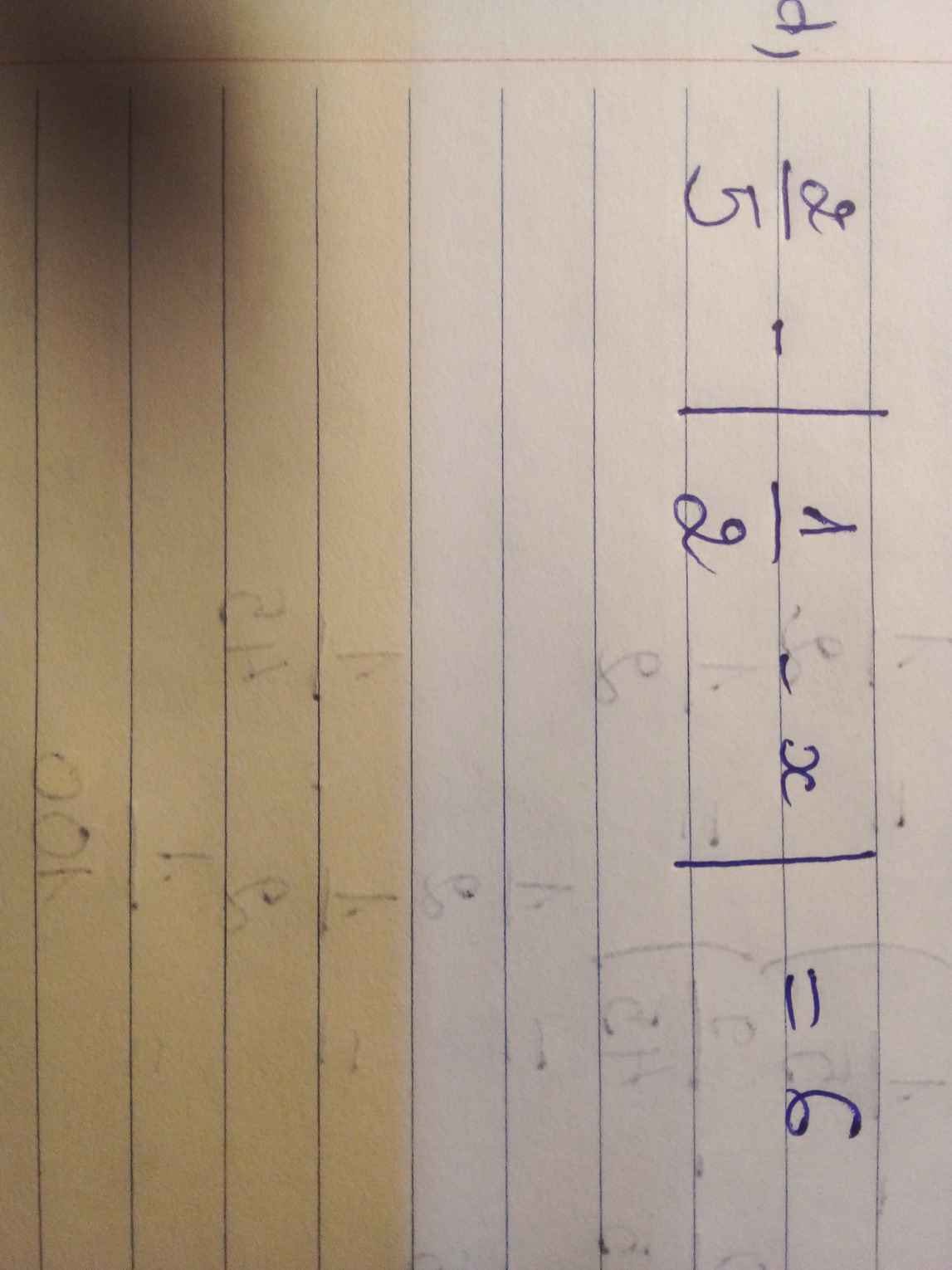



Mình không thấy rõ @@ bạn viết ra được không?