Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
NM là dây
E là trung điểm của NM(gt)
Do đó: OE⊥MN tại E(Định lí đường kính vuông góc với dây)
Xét tứ giác OEAC có
\(\widehat{OEA}+\widehat{OCA}=180^0\)
nên OEAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay O,E,A,C cùng nằm trên 1 đường tròn(1)
Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
nên OBAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay O,B,A,C cùng nằm trên 1 đường tròn(2)
Từ (1) và (2) suy ra A,B,O,E,C cùng nằm trên 1 đường tròn

a: BA là tiếp tuyến của (O) có B là tiếp điểm
=>OB\(\perp\)BA tại B
=>ΔOBA vuông tại B
ΔBOA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là tia phân giác của \(\widehat{BOC}\)
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OCA}=\widehat{OBA}=90^0\)
=>AC là tiếp tuyến của (O)
c: Xét ΔABO vuông tại B có \(sinBAO=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
ΔOBA=ΔOCA
=>\(\widehat{BAO}=\widehat{CAO}\) và AB=AC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều
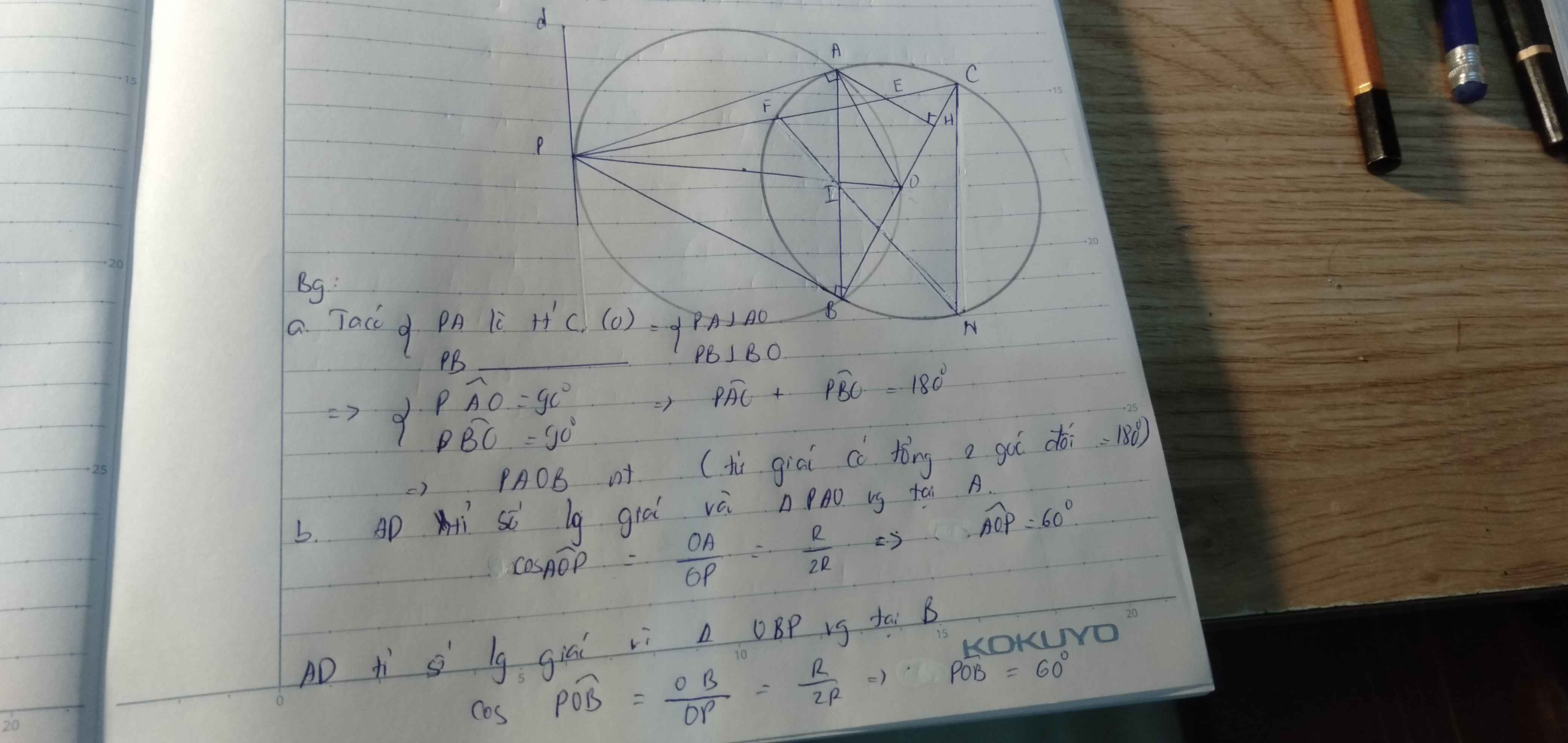
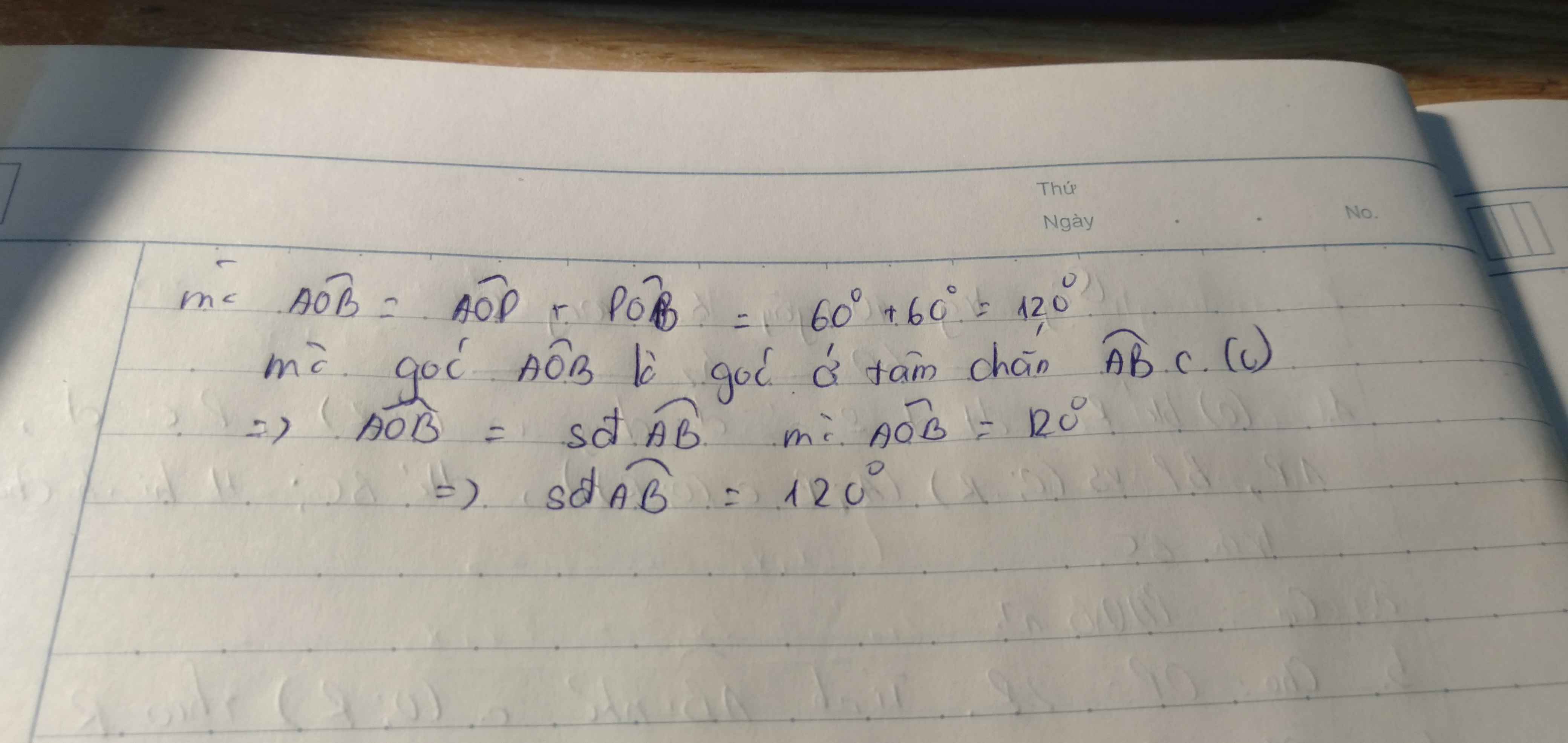
Xét ΔOAP vuông tại A có cos AOP=OA/OP=1/2
=>góc AOP=60 đọ
=>góc AOB=120 độ
độ dài cung nhỏ AB là:
\(\dfrac{pi\cdot R\cdot120}{180}=\dfrac{2}{3}\cdot pi\cdot R\)