K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
6 tháng 8 2021
a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
6 tháng 8 2021
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
NT
3 tháng 8 2021
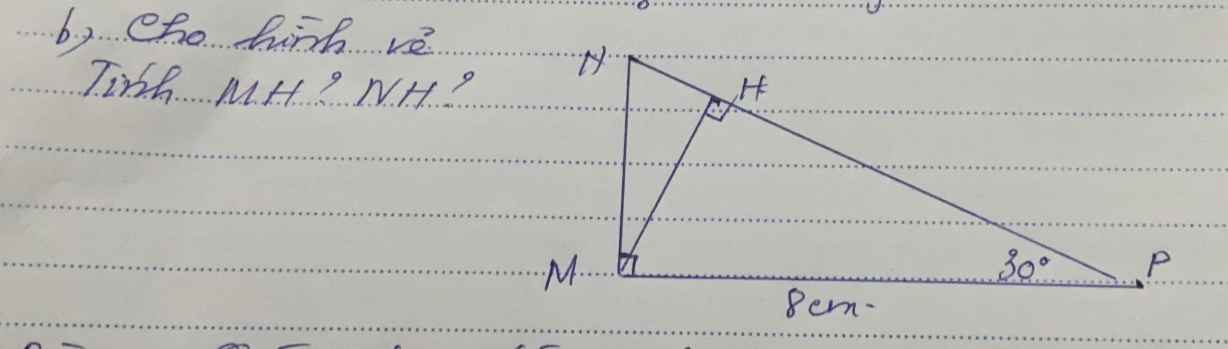
Áp dụng tỉ số lượng giác của góc nhọn vào \(\Delta MHP\), ta có:
\(\cos30\text{°}=\dfrac{MH}{8}\Rightarrow MH=8.\cos30\text{°}=4\sqrt{3}\left(cm\right)\)
Mặt khác, \(\text{∠}MNP=90\text{°}-30\text{°}=60\text{°}\)
Áp dụng tí số lượng giác của góc nhọn vào \(\Delta MHN\), ta có:
\(\tan60\text{°}=\dfrac{4\sqrt{3}}{NH}\Rightarrow NH=4\sqrt{3}.\tan60\text{°}=12\left(cm\right)\)
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
Xét tam giác $MHP$ vuông tại $H$ thì:
$\frac{MH}{MP}=\sin P=\sin 30^0=\frac{1}{2}$
$\Rightarrow MH=\frac{MP}{2}=4$ (cm)
Theo định lý Pitago:
$HP=\sqrt{MP^2-MH^2}=\sqrt{8^2-4^2}=4\sqrt{3}$
Theo hệ thức lượng trong tam giác vuông:
$MH^2=NH.HP$
$\Leftrightarrow 4^2=4\sqrt{3}.NH$
$\Leftrightarrow NH=\frac{4\sqrt{3}}{3}$ (cm)
20 tháng 1 2022
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
b: Xét ΔOCI và ΔOAI có
OC=OA
\(\widehat{COI}=\widehat{AOI}\)
OI chung
Do đó: ΔOCI=ΔOAI
Suy ra: \(\widehat{OCI}=\widehat{OAI}=90^0\)
hay IA là tiếp tuyến của (O)
21 tháng 7 2023
a: ĐKXĐ: x>=0; x<>1
\(K=\dfrac{1+\sqrt{x}-1}{\sqrt{x}-1}\cdot\left(\sqrt{x}-1\right)\cdot\left(-\sqrt{x}\right)\)
=-x
b: K>=x^3
=>x^3<=-x
=>x^3+x<=0
=>x(x^2+1)<=0
=>x<=0
=>x=0
21 tháng 12 2021
a: Xét hình thang ADCB có
O là trung điểm của AB
OM//AD//CB
Do đó: M là trung điểm của CD
hay MC=MD
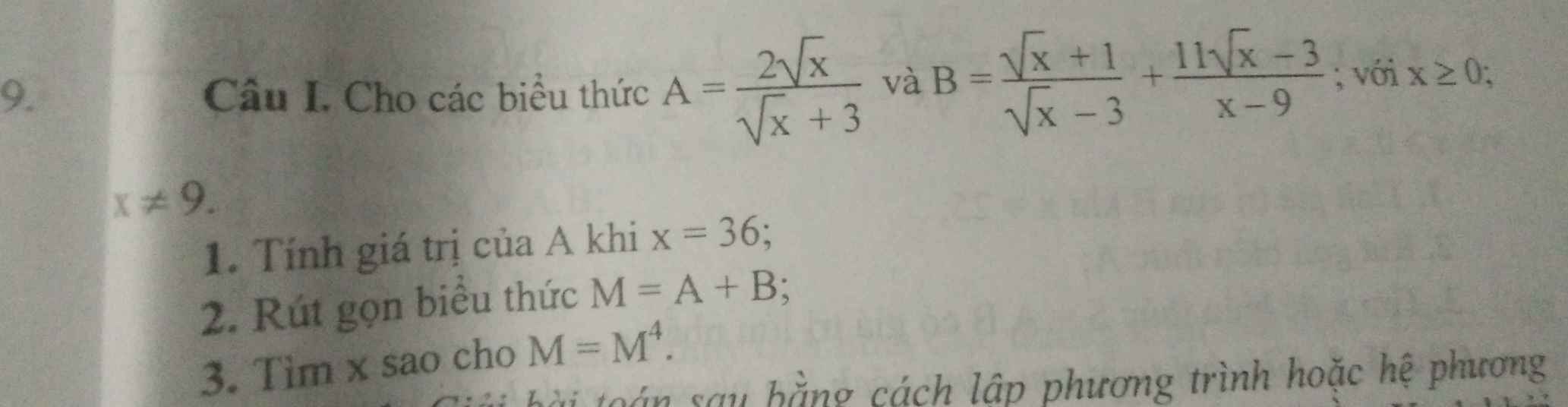
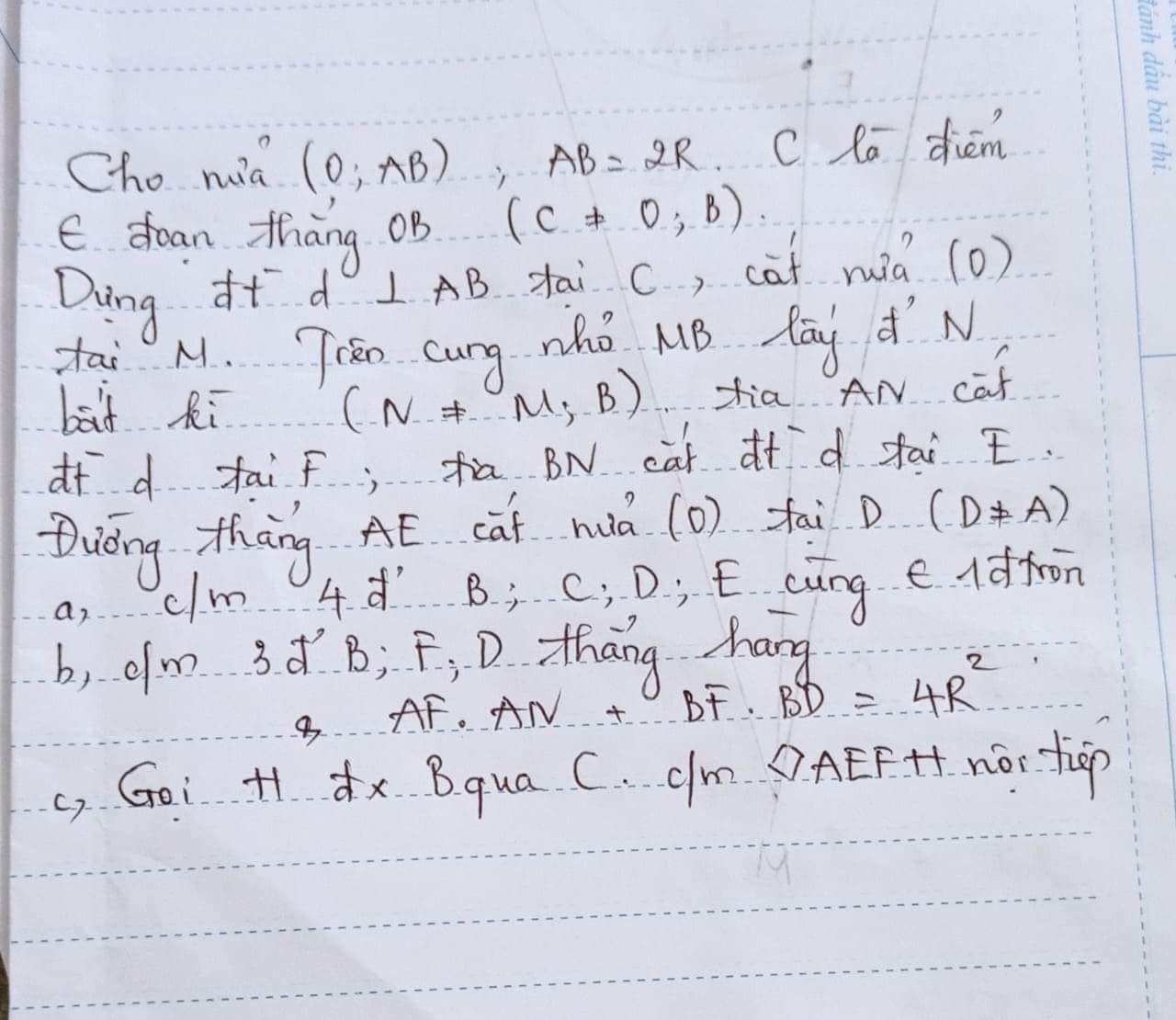
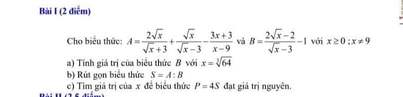
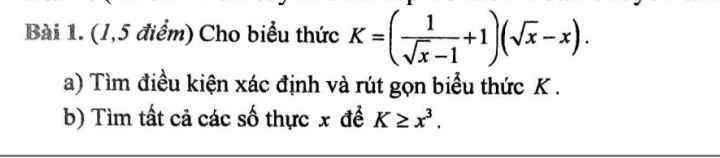
1) Thay \(x=16\)vào B ta đc
\(\frac{16-\sqrt{16}}{\sqrt{16}-2}=6\)
Vậy B =6 với x=16
2)\(A=\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}}{2-\sqrt{x}}-\frac{2\sqrt{x}+8}{x-4}\)
\(=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{x-4}-\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}-\frac{2\sqrt{x}+8}{x-4}\)
\(=\frac{x-\sqrt{x}-2}{x-4}-\frac{x+2\sqrt{x}}{x-4}-\frac{2\sqrt{x}+8}{x-4}\)
\(=\frac{-5\sqrt{x}-10}{x-4}\)
\(=\frac{-5\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\frac{-5}{\sqrt{x}-2}\)
3) Để \(B-A< 0\)\(\Leftrightarrow\frac{x-\sqrt{x}}{\sqrt{x}-2}-\frac{-5}{\sqrt{x}-2}< 0\)
\(\Leftrightarrow\frac{x-\sqrt{x}+5}{\sqrt{x}-2}< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-\sqrt{x}+5>0\\\sqrt{x}-2< 0\end{cases}}\)( vì \(x-\sqrt{x}+5>0;\forall x\))
\(\Leftrightarrow x< 4\) Kết hợp với điều kiện đề bài
\(\Rightarrow0\le x< 4\) Mà x nguyên
\(\Rightarrow x\in\left\{0;1;2;3\right\}\)
Vậy ...