
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\) Xét \(\Delta AEM\) vuông tại E và \(\Delta AFM\) vuông tại F:
\(\widehat{EAM}=\widehat{FAM}\) \((\)AM là phân giác \(\widehat{BAC}\)\().\)
\(AM\) \(chung.\)
\(\Rightarrow\) \(\Delta AEM\) \(=\Delta AFM\left(ch-gn\right).\)
\(b.\) Xét \(\Delta BEM\) vuông tại E:
BE; EM là 2 cạnh góc vuông.
BM là cạnh huyền.
\(\Rightarrow\) \(BM>BE;ME.\)
Vì \(\Delta AEM\) \(=\Delta AFM\left(cmt\right).\)
\(\Rightarrow ME=MF\) (2 cạnh tương ứng).
Mà \(BM>ME.\)
\(\Rightarrow BM>MF.\)

Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2

Ta có:
( -64 )7 = ((-4)4)7 = (-4)28 = 428
( -16)11 = (42)11 = 422
Vì 428 > 422 nên (-64)7 > (-16)11
( chỗ có 2 dấu ngoặc tròn"(" thì thay bằng dấu ngoặc vuông nha )
ta so sánh :
647 và 1611
647 = ( 43 )7 = 421
1611 = ( 42 )11 = 422
\(\Rightarrow\)647 < 1611
\(\Rightarrow\)( -64 )7 > ( -16 )11

Tên tam giác là MNP
Tên 3 đỉnh là M,N,P
Tên 3 góc là \(\widehat{mNp};\widehat{nMp};\widehat{nPm}\)
Tên 3 cạnh là MN, NP, MP

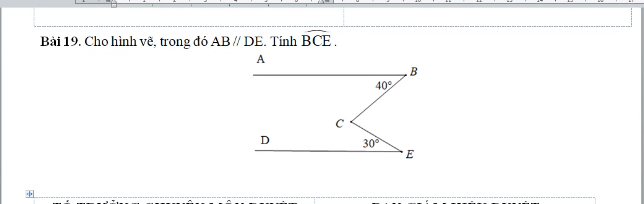
Kẻ CF//AB thì CF//DE
Do đó \(\widehat{BCF}=\widehat{ABC}=40^0;\widehat{FCE}=\widehat{CED}=30^0\) (so le trong)
Vậy \(\widehat{BCE}=\widehat{BCF}+\widehat{FCE}=30^0+40^0=70^0\)

Để ;(x + 1).(x - 3) < 0 thì ta có 2 trường hợp
Th1 : \(\hept{\begin{cases}x+1< 0\\x-3>0\end{cases}\Rightarrow\hept{\begin{cases}x< -1\\x>3\end{cases}\left(loai\right)}}\)
Th2 : \(\hept{\begin{cases}x+1>0\\x-3< 0\end{cases}\Rightarrow\hept{\begin{cases}x>-1\\x< 3\end{cases}\Rightarrow}-1< x< 3}\)


 giúp mk với mn mk đang gấp
giúp mk với mn mk đang gấp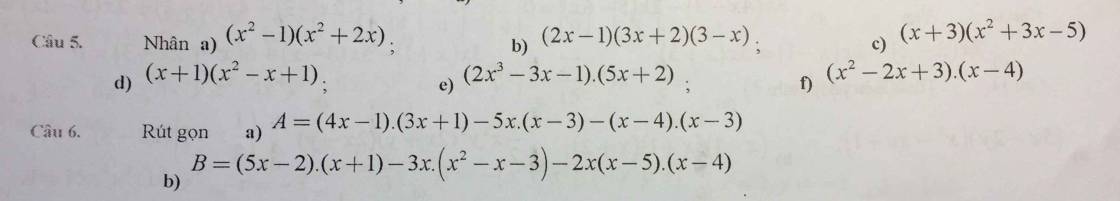
 giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
 giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
Câu 5:
\(A\ge-1\forall x\)
Dấu '=' xảy ra khi x=2
Câu 5:
Ta thấy \(\left(x-2\right)^2\ge0\Rightarrow A\ge-1\)
Dấu "=" xảy ra khi \(\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)