K
Khách
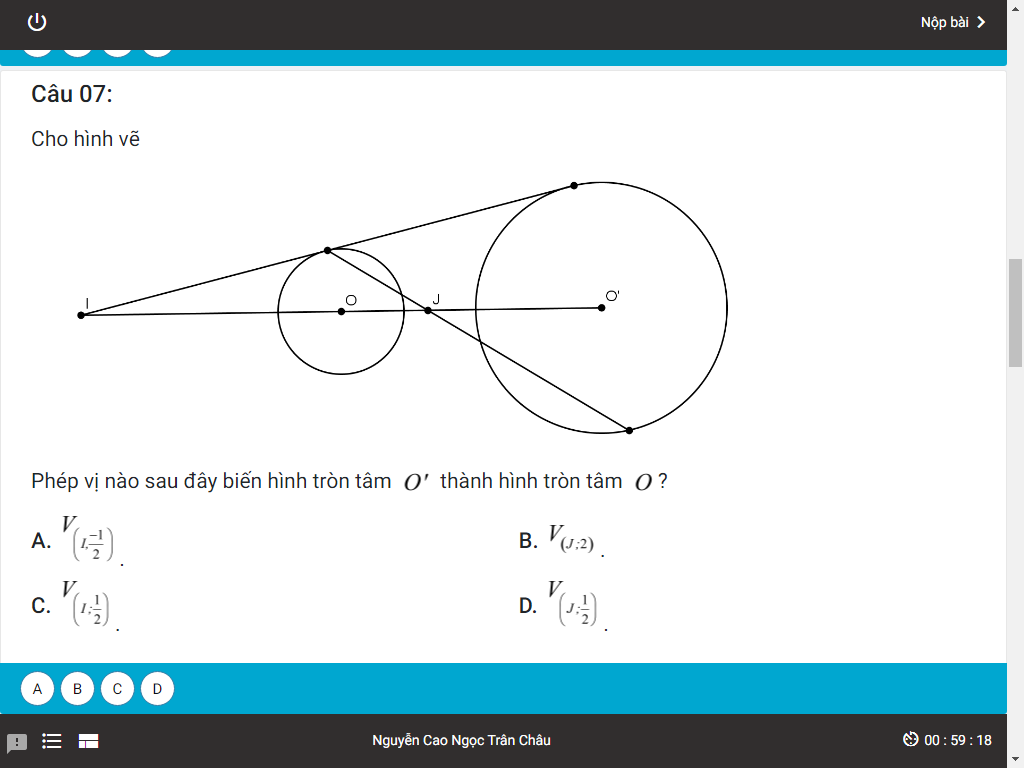
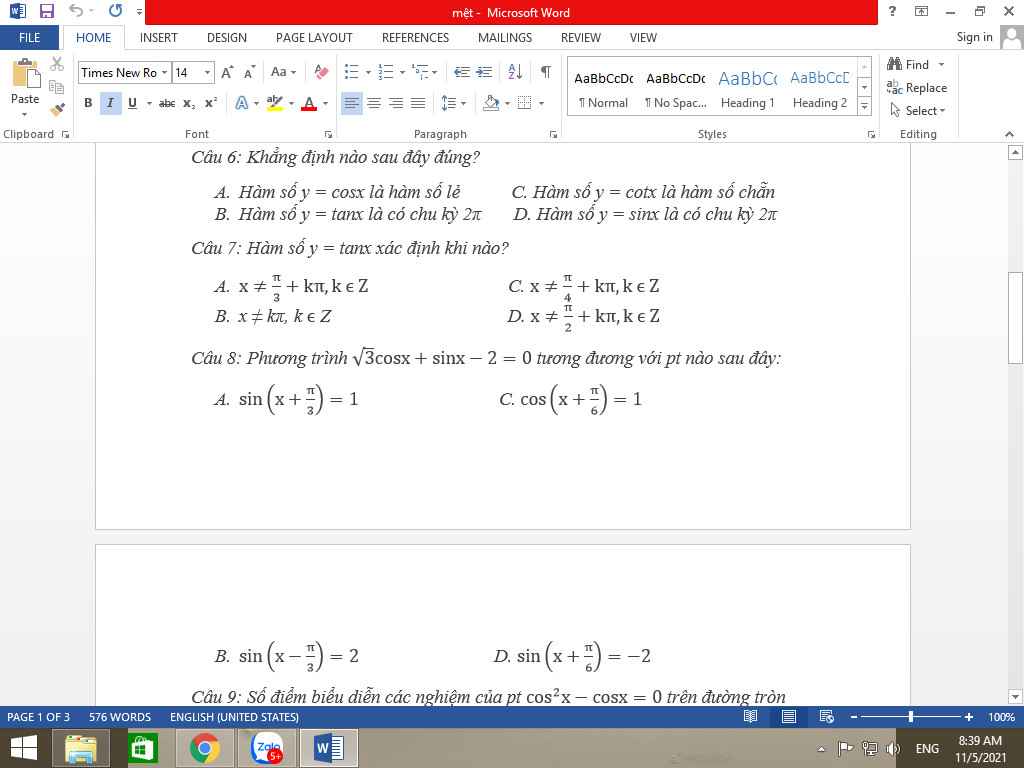
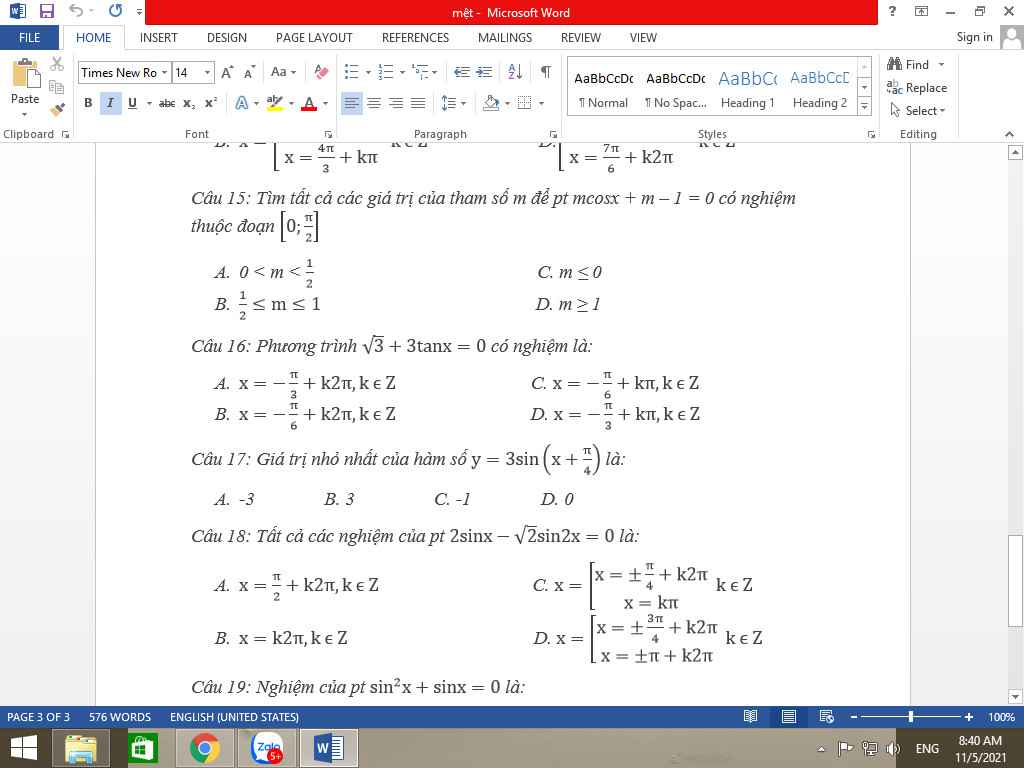
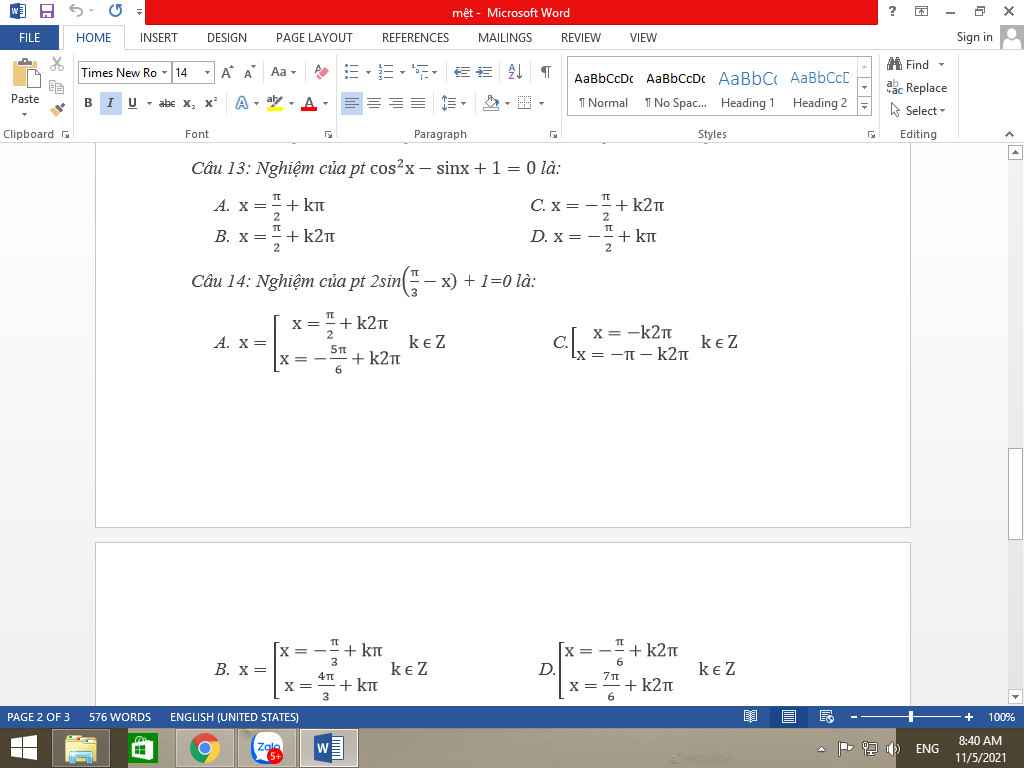
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TC
5 tháng 11 2021
giải hình nào cx đc nha ko cần giải hết đâu
ai giải hết thì tym sập nhà
ai giải 1 ảnh thì tym 3tus
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2021
Chia nhỏ ra, gửi từng hình 1 thôi em
Nhiều quá kéo chuột đã thấy mòn con chuột rồi
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 12 2018
Không gian mẫu: \(n\left(\Omega\right)=C_{16}^3=560\)
Gọi O là tâm (H), chọn 2 đỉnh của (H) sao cho đoạn thẳng nối chúng đi qua O có 8 cách chọn (1)
Với mỗi đỉnh còn lại của (H), chúng sẽ cùng với hai điểm ở (1) tạo thành một tam giác vuông \(\Rightarrow\) còn lại 14 đỉnh
\(\Rightarrow\) có \(14.8=112\) tam giác vuông
Xác suất: \(P=\dfrac{112}{560}=\dfrac{1}{5}\)
3 tháng 1 2019
\(\Leftrightarrow8\cos^3x-3\cos^2x-4\cos x+\left(1-\cos^2x\right)=0\)
\(\Leftrightarrow8\cos^3x-4\cos^2x-4\cos x+1=0\)
Sau đó ấn máy tính nhưng bài này ra nghiệm lẻ lắm bạn
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
\(a=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{x-3}=-\dfrac{1}{6}\)
\(b=\lim\limits_{x\rightarrow2}\dfrac{\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+3}{x+2}=\dfrac{5}{4}\)
\(c=\lim\limits_{x\rightarrow4}\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x+5\right)\left(x-4\right)}=\lim\limits_{x\rightarrow4}\dfrac{x+4}{x+5}=\dfrac{8}{9}\)
\(d=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+2}{x-1}=4\)
\(e=\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt{x+7}+3}=\dfrac{1}{6}\)
\(f=\lim\limits_{x\rightarrow1}\dfrac{x+3-4}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt{x+3}+2}=\dfrac{1}{4}\)
\(h=\lim\limits_{x\rightarrow-3}\dfrac{x+7-4}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{\sqrt{x+7}+2}=\dfrac{1}{4}\)
MN
5 tháng 5 2021
Bài 1:
a,
= limx->-3 \(\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}\)
= limx->3 x-3
= -3 -3
= -6
b,
= limx->2 \(\dfrac{\left(x-2\right)\left(x+3\right)}{\left(x-2\right)\left(x+2\right)}\)
= limx->2 \(\dfrac{x+3}{x+2}\)
= \(\dfrac{5}{4}\)
c,
= limx->4 \(\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)\left(x+5\right)}\)
= limx->4 \(\dfrac{\left(x+4\right)}{\left(x+5\right)}\)
= \(\dfrac{8}{9}\)
d,
= limx->2 \(\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x-1\right)}\)
= limx->2 \(\dfrac{\left(x+2\right)}{\left(x-1\right)}\)
= 4
