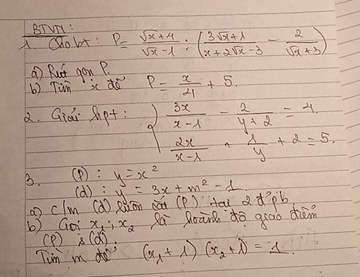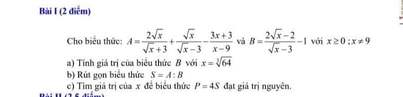K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 6 2023
3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8
26 tháng 6 2021
1. \(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\dfrac{2}{\sqrt{x}+3}\right)\)
\(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{3\sqrt{x}+1-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\right)\)
\(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{3\sqrt{x}+1-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\right)\)
\(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\right)\)
\(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}.\sqrt{x}-1\)
P=\(\sqrt{x}+4\)
b) \(P=\dfrac{x}{4}+5\)
⇔\(\sqrt{x}+4=\dfrac{x}{4}+5\)
⇔\(\dfrac{x}{4}-\sqrt{x}+1=0\)
⇔\(x-4\sqrt{x}+4=0\)
⇔\(\left(\sqrt{x}-2\right)^2=0\)
⇔\(\sqrt{x}-2=0\)
⇔\(\sqrt{x}=2\)
⇔\(x=4\)
Vậy x=4 thì P=\(\dfrac{x}{4}+5\)
26 tháng 6 2021
Bài 1:
a) Ta có: \(P=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{3\sqrt{x}+1}{x+2\sqrt{x}-3}-\dfrac{2}{\sqrt{x}+3}\right)\)
\(=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\left(\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}-\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{\sqrt{x}+4}{\sqrt{x}-1}:\dfrac{\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\sqrt{x}+4\)
b) Ta có: \(P=\dfrac{x}{4}+5\)
\(\Leftrightarrow\sqrt{x}+4=\dfrac{1}{4}x+5\)
\(\Leftrightarrow\dfrac{1}{4}x-\sqrt{x}+1=0\)
\(\Leftrightarrow x-4\sqrt{x}+4=0\)
\(\Leftrightarrow x=4\)
BB
1
16 tháng 6 2021
Với \(x\ge\dfrac{5}{2}\)có: \(A=x+\sqrt{2x-5}\ge\dfrac{5}{2}+0=\dfrac{5}{2}\)
Dấu '=' xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\)
\(\Rightarrow A_{min}=\dfrac{5}{2}\)
NH
1
AH
Akai Haruma
Giáo viên
10 tháng 6 2021
Câu 15:
Gọi $x_0$ là nghiệm chung của 2 pt thì:
\(\left\{\begin{matrix}
x_0^2+ax_0+1=0\\
x_0^2-x_0-a=0\end{matrix}\right.\Rightarrow x_0(a+1)+(a+1)=0\)
\(\Leftrightarrow (x_0+1)(a+1)=0\)
Hiển nhiên $a\neq -1$ để 2 PT không trùng nhau. Do đó $x_0=-1$ là nghiệm chung của 2 PT
Thay vào:
$(-1)^2+a(-1)+1=0$
$\Leftrightarrow 1-a+1=0\Rightarrow a=2$
Đáp án C.
AH
Akai Haruma
Giáo viên
10 tháng 6 2021
Câu 16:
D sai. Trong tam giác vuông tại $A$ là $ABC$, $\cos (90^0-\widehat{B})=\cos \widehat{C}$ và không có cơ sở để khẳng định $\cos \widehat{C}=\sin \widehat{C}$
LT
7 tháng 6 2021
\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{3-11\sqrt{x}}{9-x}\)\(\left(ĐK:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}+\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
Chúc bạn học tốt ^.^
AT
7 tháng 6 2021
\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{3-11}{9-x}\left(x\ge0,x\ne9\right)\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+11\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
CC
1
13 tháng 10 2021
\(\sqrt{x-2}=3\left(x\ge2\right)\\ \Leftrightarrow x-2=9\Leftrightarrow x=11\left(tm\right)\\ \sqrt{4x^2}+4x+1=3\Leftrightarrow\left|2x\right|=2-4x\\ \Leftrightarrow\left[{}\begin{matrix}2x=2-4x\left(x\ge0\right)\\2x=4x-2\left(x< 0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\left(tm\right)\\x=1\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{1}{3}\)