K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 6 2023
a: Xét ΔEAD và ΔECG có
góc EAD=góc ECG
góc AED=góc CEG
=>ΔEAD đồng dạng với ΔECG
=>AD/CG=ED/EG
=>AD*EG=ED*CG
b: Xét ΔHEG và ΔHCB có
góc HEG=góc HCB
góc EHG=góc CHB
=>ΔHEG đồng dạng với ΔHCB
=>HE/HC=HG/HB
Xét ΔHAB và ΔHCG có
góc HAB=góc HCG
góc AHB=góc CHG
=>ΔHAB đồng dạng với ΔHCG
=>HA/HC=HB/HG
=>HC/HA=HG/HB
=>HC/HA=HE/HC
=>HC^2=HA*HE
c: HI//BA
=>HI/BA=CH/CA=CI/CB
HI//EG
=>HI/EG=BI/BC
HI/BA=CI/CB
HI/BA+HI/EG=BI/BC+CI/BC=1
=>HI(1/BA+1/EG)=1
=>1/BA+1/EG=1/HI
28 tháng 8 2021
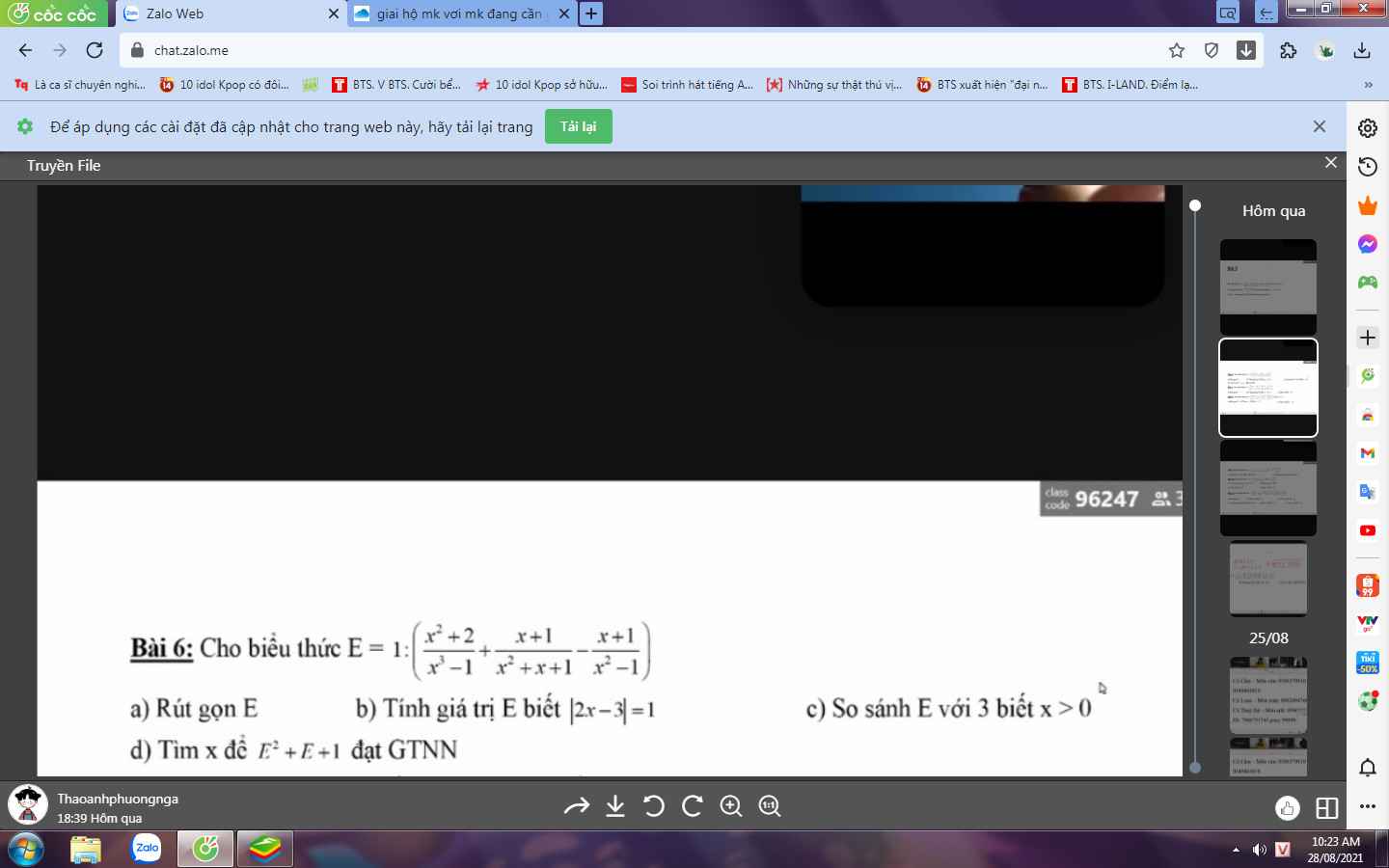
Bài 6:
a: Ta có: \(E=1:\left(\dfrac{x^2+2}{x^3-1}-\dfrac{x+1}{x^2+x+1}-\dfrac{x+1}{x^2-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\dfrac{x^2+2-x^2+1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-x^2-x+2}\)
\(=\dfrac{-\left(x-1\right)\left(x^2+x+1\right)}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-x^2-x-1}{x+2}\)
25 tháng 3 2021
Bài 5:
b) Xét tứ giác AHCK có
\(\widehat{AHC}\) và \(\widehat{AKC}\) là hai góc đối
\(\widehat{AHC}+\widehat{AKC}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AHCK là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay \(\widehat{AKH}=\widehat{ACH}\)(Cùng nhìn cạnh AH)
NT
1
9 tháng 3 2022
Bài 4:
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó:ΔABC\(\sim\)ΔHAC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=4.8\left(cm\right)\)
c: Xét ΔAHC vuông tại H có HE là đường cao
nên \(HE^2=EA\cdot EC\)
NK
Giúp mk với mọi người ơi mk đang cần gấp cảm ơn mọi người nhé
1
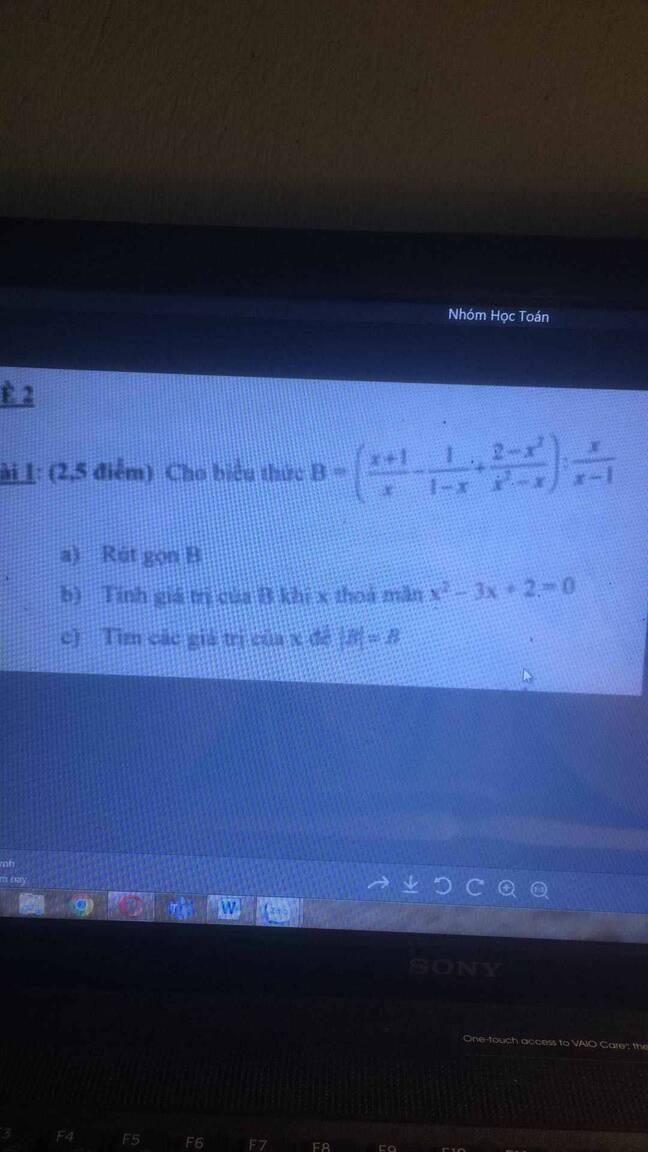
Rút gọn B ta được \(B=\dfrac{x+1}{x^2}\)
Để \(\left|B\right|=B\Leftrightarrow B\ge0\)
\(\Leftrightarrow\dfrac{x+1}{x^2}\ge0\)
\(\Leftrightarrow x\ge-1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x\ge-1\\x\ne0\\x\ne1\end{matrix}\right.\)