Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)

1.
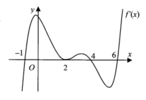
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
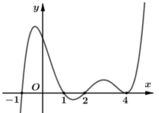
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Chọn B
f ' ( x ) = 1 - 2 s i n x c o s x = s i n 2 x + c o s 2 x - 2 . s i n x . c o s x = ( s i n x - c o s x ) 2 ≥ 0 ∀ x ∈ R
Hàm số đồng biến trên khoảng (-∞; +∞)

Đáp án C
Xét ![]()
Khi đó ![]()
![]()
(trong đó ![]() là nghiệm kép).
là nghiệm kép).
Ta có bảng xét dấu của đạo hàm ![]() như sau:
như sau:
x - ∞ -1 1/2 3/2 5/2 + ∞
y' - 0+ 0 + 0 - 0 +
Để xét dấu của y’, ta có thể xét dấu tại một điểm nào đó, ví dụ
![]()

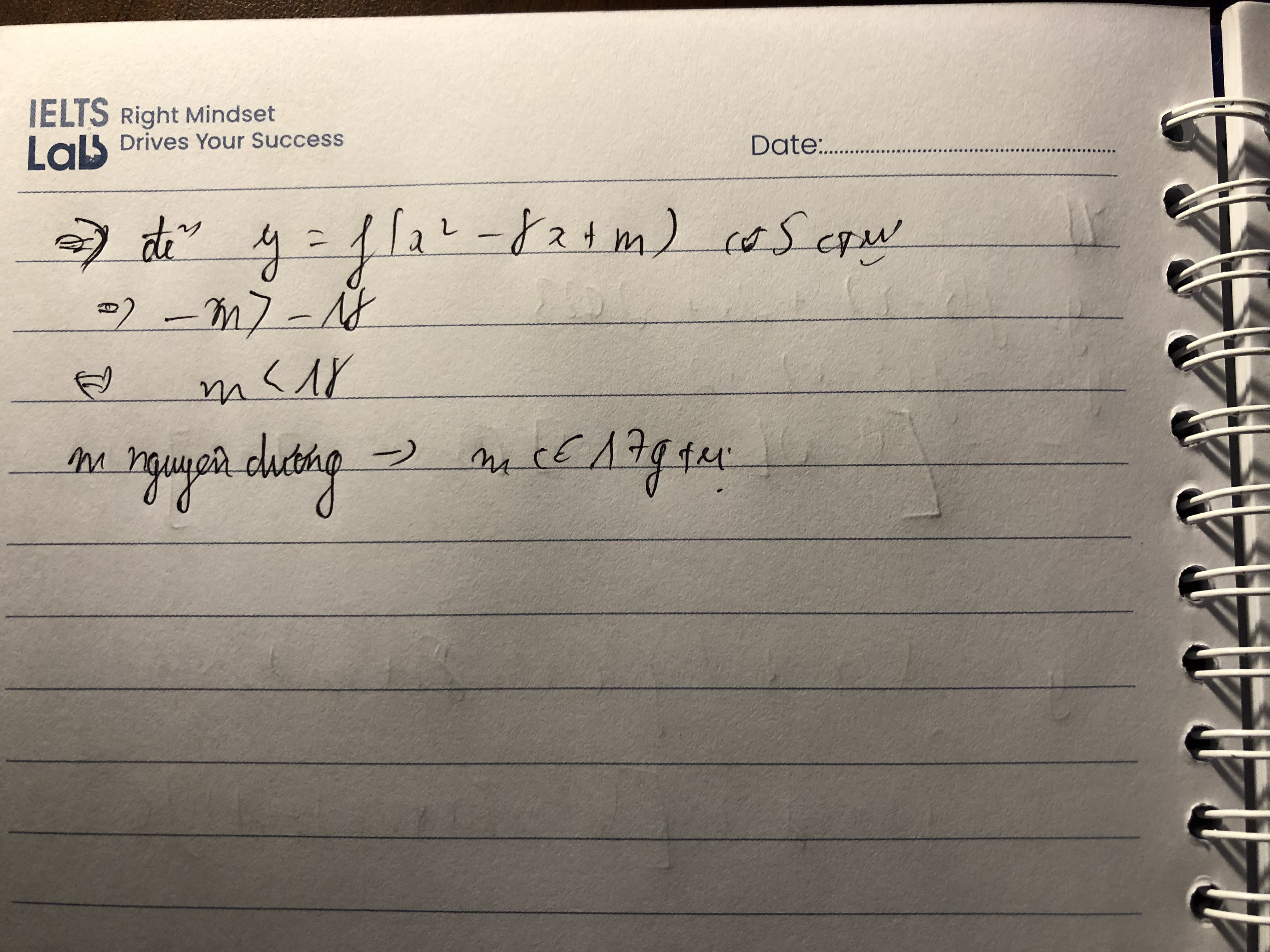
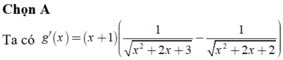

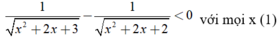



\(f'\left(x\right)=2+2sin2x\)
Ta thấy:
\(-1\le sin2x\le1\)
\(-2\le2sinx\le2\)
\(0\le2+2sin2x\le4\)
\(\Rightarrow f'\left(x\right)\ge0\forall x\)
nên hàm số đồng biến trên R
thank you