K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 10 2021
\(\left|x+\dfrac{1}{3}\right|-4=-1\)
\(\Leftrightarrow\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
27 tháng 1 2022
Bài 3:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
mà DE<DC
nên DA<DC
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC
hay ΔBFC cân tại B
d: Ta có: BF=BC
nên B nằm trên đường trung trực của BC(1)
Ta có: DF=DC
nên D nằm trên đường trung trực của BC(2)
Ta có: KF=KC
nên K nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra B,D,K thẳng hàng
NT
1
12 tháng 1 2023
a: góc ACB=180-50-65=65 độ
b: góc yAC=180-50=130 độ
góc yAx=góc ABC=65 độ=1/2*góc yAC
=>Ax là phân giác của góc yAC
NM
1
12 tháng 1 2022
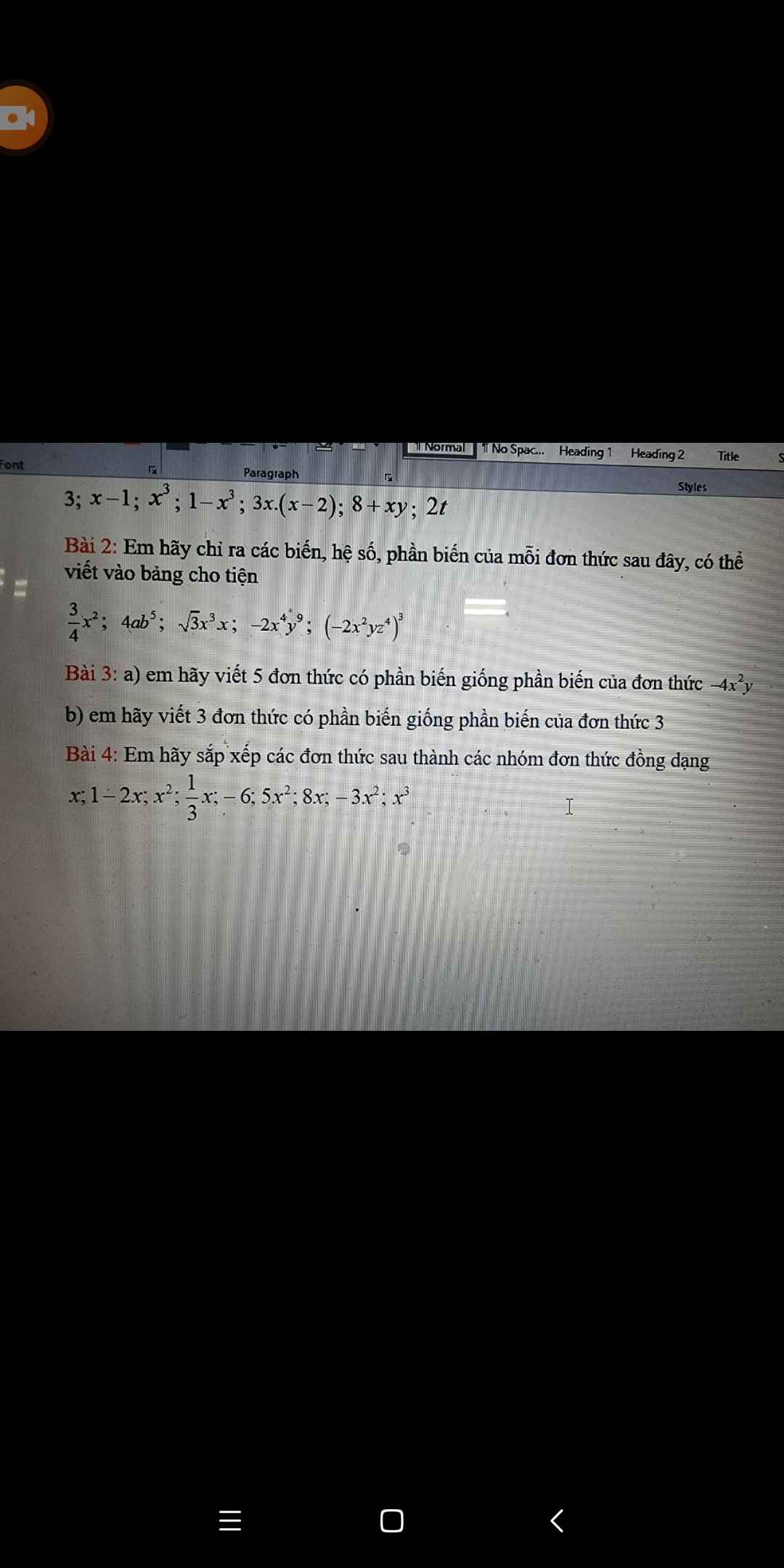
Bài 4:
Nhóm 1: x;1/3x; 8x
Nhóm 2: \(x^2;5x^2;-3x^2\)
27 tháng 6 2023
4:
a: Xét ΔADH vuông tại D và ΔHEA vuông tại E có
AH chung
góc HAD=góc AHE
=>ΔADH=ΔHEA
=>DH=EA
b: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
mà AH cắt DE tại I
nên IA=IH=ID=IE
c: ADHE là hình chữ nhật
=>góc ADE=góc AHE
mà góc AHE=góc ACB
nên góc ADE=góc ACB
mk vs ạ
8 tháng 8 2023
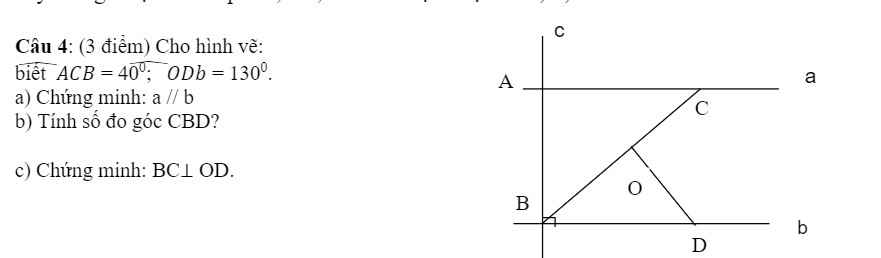
Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
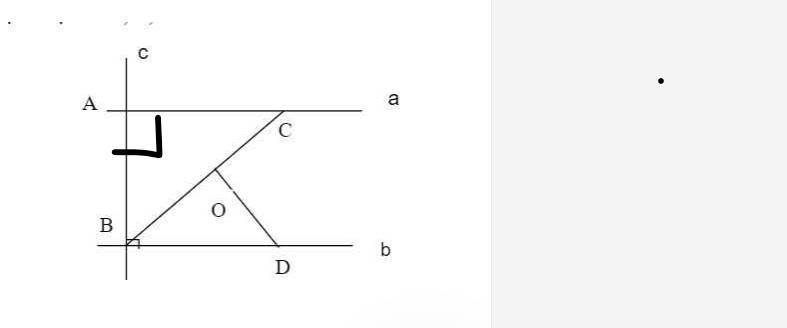
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Giúp mk vs ạ
PC
29 tháng 5 2016
Bài 30:
a.
x2+5x=0x2+5x=0
x(x−5)=0x(x−5)=0
- x=0x=0
- x−5=0x−5=0
x=5x=5
Vậy x = 0 và x = 5 là nghiệm của đa thức trên.
b.
3x2−4x=03x2−4x=0
x(3x−4)=0x(3x−4)=0
- x=0x=0
- 3x−4=03x−4=0
3x=43x=4
x=43x=43
Vậy x = 0 và x = 4/3 là nghiệm của đa thức trên.
c.
5x5+10x=05x5+10x=0
5x(x4+2)=05x(x4+2)=0
- 5x=05x=0
x=0x=0
- x4+2=0x4+2=0
x4=−2x4=−2
mà x4≥0x4≥0 với mọi x => loại
Vậy x = 0 là nghiệm của đa thức trên.
d.
x3+27=0x3+27=0
x3=−27x3=−27
x3=(−3)3x3=(−3)3
x=−3x=−3
Vậy x = - 3 là nghiệm của đa thức trên.
Chúc bạn học tốt
29 tháng 5 2016
29. a) Giả sử f(x) = 0
=> x3 - x2 + x - 1 = 0
=> x2.(x - 1) + (x - 1) = 0
=> (x - 1).(x2 + 1) = 0
=> x - 1 = 0 (x2 + 1 khác 0)
=> x = 1
Vậy 1 nghiệm của đa thức là 1.
b. Giả sử g(x) = 0
=> 11x3 + 5x2 +4x + 10 = 0
=> 10x3 + x3 + 4x2 + x2 + 4x + 10 = 0
=> (10x3 + 10) + (x3 + x2) + (4x2 + 4x) = 0
=> 10.(x3 + 1) + x2.(x + 1) + 4x.(x + 1) = 0
=> 10.(x + 1).(x2 - x + 1) + x2.(x + 1) + 4x.(x + 1) = 0
=> (x + 1).[10.(x2 - x + 1) + x2 + 4x] = 0
=> x + 1 = 0
=> x = -1
Vậy 1 nghiệm của g(x) là -1.
c. Giả sử h(x) = 0
=> -17x3 + 8x2 - 3x + 12 = 0
=> (-17x3 + 17x2) - (9x2 - 9x) - (12x - 12) = 0
=> -17x2.(x - 1) - 9x.(x - 1) - 12.(x - 1) = 0
=> (x - 1).(-17x2 - 9x - 12) = 0
=> x - 1 = 0
=> x = 1
Vậy 1 nghiệm của h(x) là 1.
giúp mình bài 4 vs ạ
Bài 4:
a: Xét ΔBAE có
BH là đường phân giác
BH là đường cao
Do đó: ΔBAE cân tại B
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
DO đó: ΔBAD=ΔBED
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay ED\(\perp\)BC
c: Ta có: ΔBAD=ΔBED
nên DA=DE
mà DE<DC
nên DA<DC