
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2 :
Bài 2 :
a, \(A=6x^3y^6z\)hệ số 6 ; biến x^3y^6z ; bậc 10
b, \(B=-\dfrac{2}{3}xy^2\left(9x^4y^2\right)=-6x^5y^4\)
hệ số -6 ; biến x^5y^4 ; bậc 9
Bài 3 :
\(A=3,5xy^2\) ta có \(x=\left|-2\right|=2;y=-1\)
Thay vào ta đc
A = 3,5 . 2 . 1 = 7

b) Xét ΔABM và ΔICM có
MA=MI(gt)
\(\widehat{AMB}=\widehat{IMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔABM=ΔICM(c-g-c)
Suy ra: \(\widehat{ABM}=\widehat{ICM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{ICM}\) là hai góc ở vị trí so le trong
nên CI//AB(Dấu hiệu nhận biết hai đường thẳng song song)

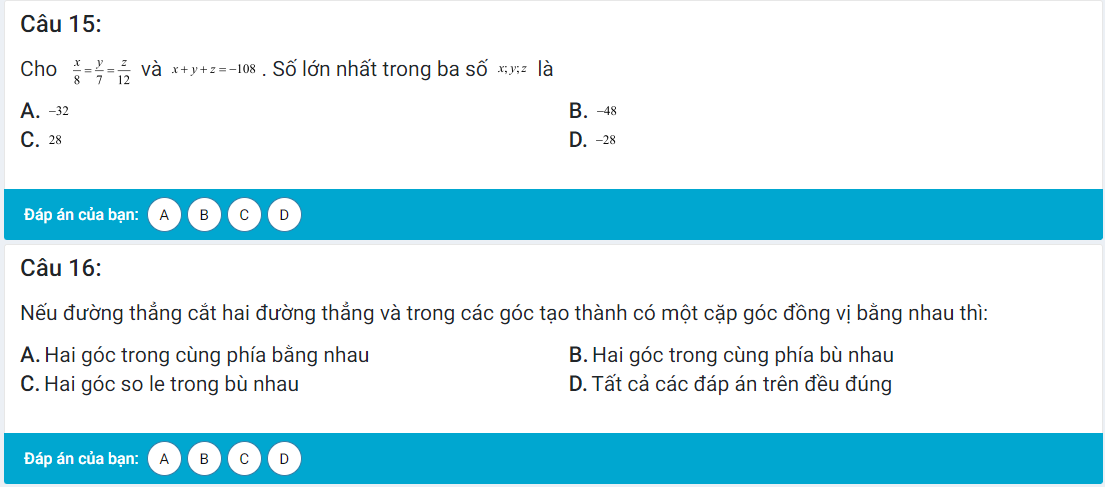
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{6}=\dfrac{a+b+c}{4+5+6}=\dfrac{75}{15}=5\)
Do đó: a=20; b=25; c=30
Gọi số hoa đạt được của An, Bình, Cường lần lượt là x; y; z
Mà x; y; z lần lượt tỉ lệ với 4; 5; 6 nên
Theo đề bài, ta có: \(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\) và x; y; z ∈ N*; ≠ 0
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{4+5+6}=\dfrac{75}{15}=5\)
=> x = 5.4 = 20.
=> y = 5.5 = 25.
=> z = 5.6 = 30.

M=(2x^2y-xy)+(2x^2y+1-3xy)
M=2x^2y-xy+2x^2y+1-3xy
M=(2x^2y+2x^2y)+(-xy-3xy)+1
M=4x^2y-4xy+1
Bac cua da thuc M la:3



a, Kẻ Oz//Ax//By
Ta có \(\widehat{zOA}=\widehat{xAO}=35^0\left(so.le.trong\right);\widehat{zOC}=180^0-\widehat{OCy}=20^0\left(trong.cùng.phía\right)\)
\(\Rightarrow\widehat{AOC}=\widehat{zOA}+\widehat{zOC}=35^0+20^0=55^0\)
b, OA ko vuông góc OC vì \(\widehat{AOC}=55^0\ne90^0\)

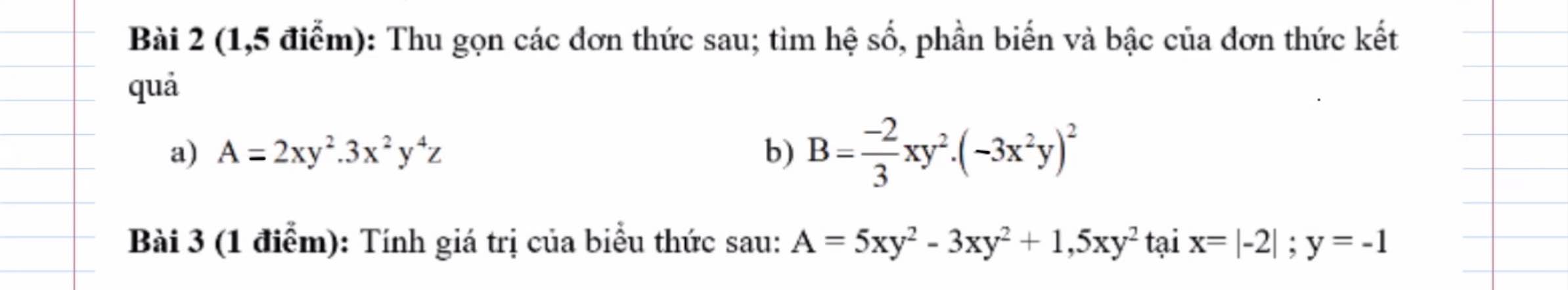



 Giúp mình vs ạ
Giúp mình vs ạ 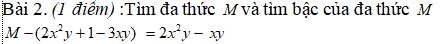

Câu 9 : Chọn C
Câu 10 :
Gọi các cạnh của tam giác lần lượt là a ; b và c lần lượt tỉ lệ với 4 ; 5 ; 3
Theo bài ra , ta có :
a + b + c = 120
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{3}=\frac{a+b+c}{4+5+3}=\frac{120}{12}=10\)
\(\Rightarrow\hept{\begin{cases}a=10.4=40\\b=10.5=50\\c=10.3=30\end{cases}}\)
=> Cạnh nhỏ nhất có giá trị là 30 m
=> Chọn B