K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1
O
25 tháng 3 2022
a) \(\dfrac{3}{4}+\dfrac{9}{5}\div\dfrac{3}{2}-1=\dfrac{3}{4}+\dfrac{18}{15}-1=\dfrac{39}{20}-1=\dfrac{19}{20}\)
b) \(\dfrac{6}{7}\cdot\dfrac{8}{13}+\dfrac{6}{13}\cdot\dfrac{9}{7}-\dfrac{4}{13}\cdot\dfrac{6}{7}=\dfrac{48}{91}+\dfrac{54}{91}-\dfrac{24}{91}=\dfrac{48+51-24}{91}=\dfrac{78}{91}=\dfrac{6}{7}\)
c) \(\dfrac{-3}{7}+\left(\dfrac{3}{-7}-\dfrac{3}{-5}\right)\)\(=\dfrac{-3}{7}+\left(\dfrac{-3}{7}-\dfrac{-3}{5}\right)=\dfrac{-3}{7}+\dfrac{6}{35}=-\dfrac{9}{35}\)
TB
1
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
đây bạn😀
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
4 tháng 1 2022
a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)
24 tháng 11 2021
Ta có : |x - 2| ; |x - 5| ; |x - 18| ≥0∀x∈R≥0∀x∈R
=> |x - 2| + |x - 5| + |x - 18| ≥0∀x∈R≥0∀x∈R
=> D có giá trị nhỏ nhất khi x = 2;5;18
Mà x ko thể đồng thời nhận 3 giá trị
Nên GTNN của D là : 16 khi x = 5 ok nha bạn
24 tháng 11 2021
x^2/x-1 = x^2-4x+4/x-1 + 4 = (x-2)^1/x-1 + 4 >= 4
Dấu "=" xảy ra <=> x-2 = 0 <=> x = 2 (tm)
Vậy GTNN của x^2/x-1 = 4 <=> x= 2
k mk nha
25 tháng 8 2021
1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân
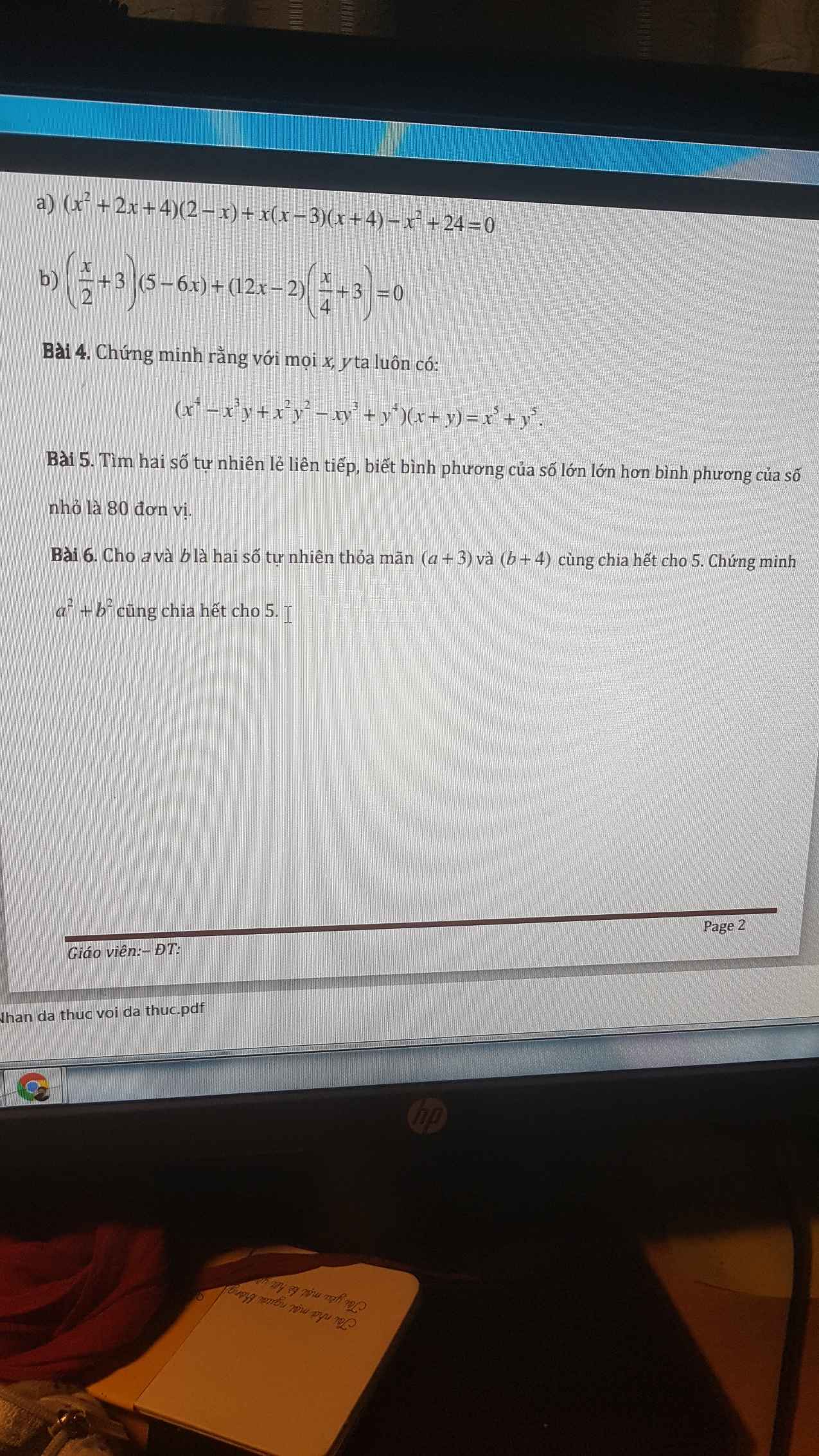
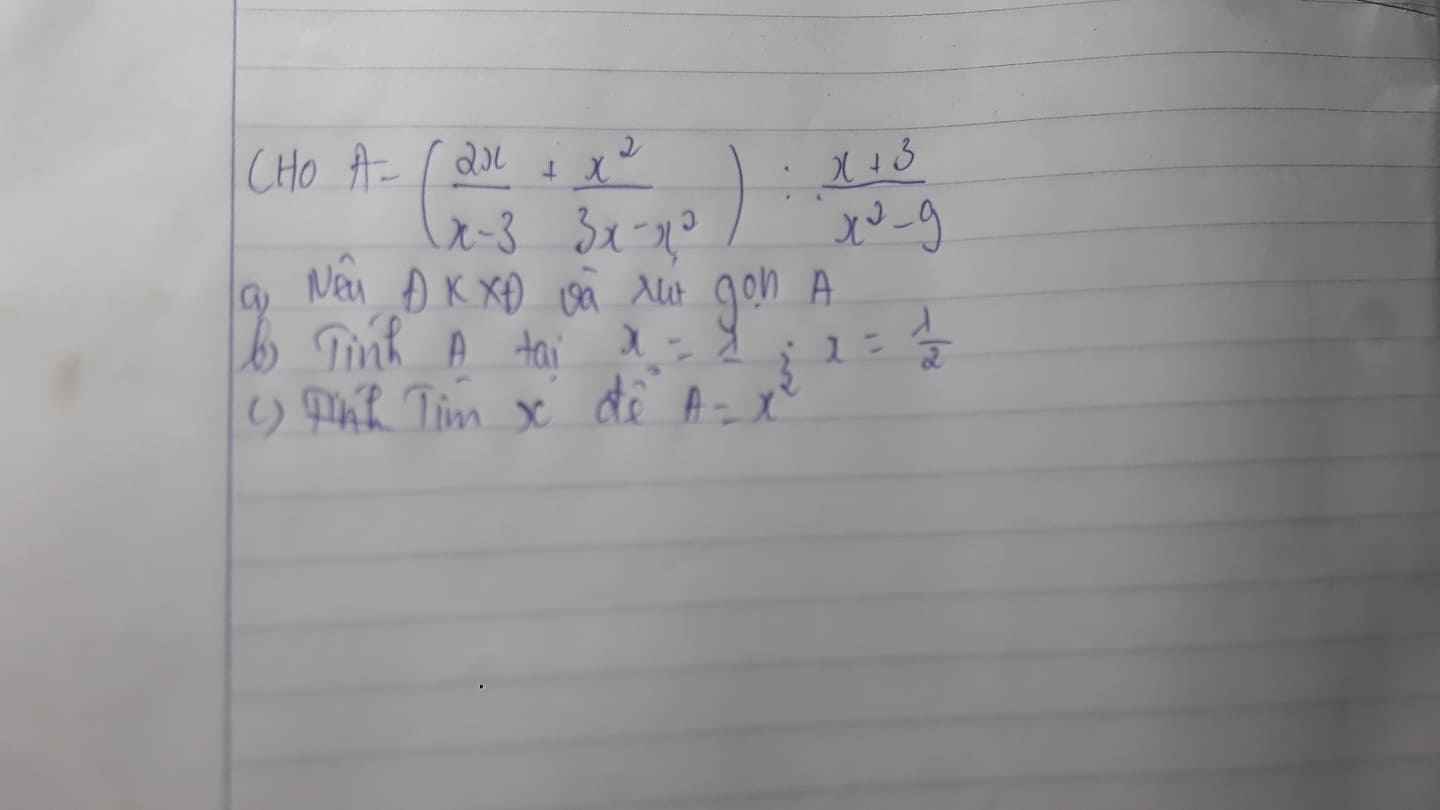
Câu 1 :
a, \(x^3-9x=x\left(x^2-9\right)=x\left(x-3\right)\left(x+3\right)\)
b, \(x^2-25+y^2-2xy=\left(x-y\right)^2-25=\left(x-y-5\right)\left(x-y+5\right)\)
c, \(x^2+2x=0\Leftrightarrow x\left(x+2\right)=0\Leftrightarrow x=0;-2\)
d, \(\left(x+2\right)^2-x\left(x+3\right)=10\)
\(\Leftrightarrow x^2+4x+4-x^2-3x-10=0\)
\(\Leftrightarrow x-6=0\Leftrightarrow x=6\)
Câu 2 :
a, \(\left(x^2-4y^2\right):\left(x+2y\right)=\left(x-2y\right)\left(x+2y\right):\left(x+2y\right)=x-2y\)
b, \(\frac{-2x}{x-5}-\frac{10}{5-x}=\frac{-2x}{x-5}+\frac{10}{x-5}=\frac{-2x+10}{x-5}=\frac{-2\left(x-5\right)}{x-5}=-2\)
c, \(\frac{3x-3}{x+2}.\frac{x^2-4}{x^2-1}=\frac{3\left(x-1\right)\left(x-2\right)\left(x+2\right)}{\left(x+2\right)\left(x-1\right)\left(x+1\right)}=\frac{3\left(x-2\right)}{x+1}\)