K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
TN
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1
1 tháng 11 2021
a: AC=12(cm)
\(\sin\widehat{C}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(\Leftrightarrow C=37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
NP
1
9 tháng 7 2023
b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO
DT
1
26 tháng 7 2023
1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17
18 tháng 9 2021
\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$
1 tháng 11 2021
b: \(BC\cdot\sin B\cdot\sin C\)
\(=BC\cdot\dfrac{AC}{BC}\cdot\dfrac{AB}{BC}\)
\(=\dfrac{BC\cdot AH\cdot BC}{BC^2}=AH\)
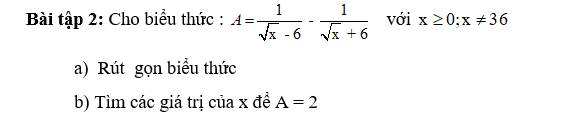
Lời giải:
a.
\(A=\frac{\sqrt{x}+6-(\sqrt{x}-6)}{(\sqrt{x}+6)(\sqrt{x}-6)}=\frac{12}{x-36}\)
b.
Để $A=2\Leftrightarrow \frac{12}{x-36}=2$
$\Leftrightarrow x-36=6\Leftrightarrow x=42$ (thỏa mãn)