Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

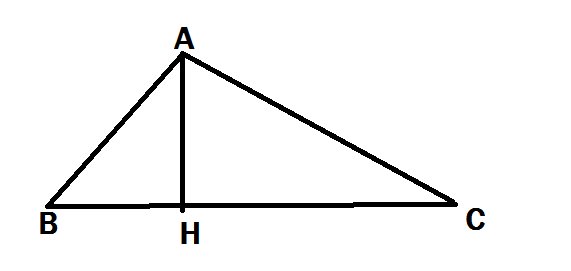
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{9}=\dfrac{1}{AB^2}+\dfrac{1}{25}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{16}{225}\)
\(\Leftrightarrow AB=\dfrac{15}{4}\)
- \(AH.BC=AB.AC\)
\(3.BC=\dfrac{15}{4}.5\)
\(BC=6,25\)
- \(CH=\dfrac{AC^2}{BC}=4\)
=> BH = 6,25 - 4 = 2,25

a/
\(BC=\sqrt{AB^2+AC^2}\) (Pitago)
\(\Rightarrow BC=\sqrt{10^2+15^2}=\sqrt{325}=5\sqrt{13}\)
\(AB^2=HB.BC\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{10^2}{5\sqrt{13}}=\dfrac{20\sqrt{13}}{13}\)
\(HC=BC-HB=5\sqrt{13}-\dfrac{20\sqrt{13}}{13}\)
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
Bạn tự thay số tính nốt nhé vì số hơi lẻ
b/
Áp dụng tính chất đường phân giác trong tg: đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn thẳng ấy
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{AB}{BC}=\dfrac{10}{5\sqrt{13}}=\dfrac{2\sqrt{13}}{13}\)
Mà \(IA+IC=AC=15\) Từ đó tính được IA và IC
Xét tg vuông ABI có
\(BI=\sqrt{AB^2+IA^2}\) (pitago)
Bạn tự thay số tính nhé

d) Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
hay \(\widehat{B}\simeq53^0\)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=70^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{C}=37^0\)

Ta có:
\(AB+BC=AC\sqrt{3}\)
=> \(\frac{AC}{BC}\sqrt{3}-\frac{AB}{BC}=1\)
=> \(\sqrt{3}\cos\widehat{C}-\sin\widehat{C}=1\)
=> \(\sqrt{3}\cos\widehat{C}-1=\sin\widehat{C}\)
Mặt khác: \(\sin^2\widehat{C}+\cos^2\widehat{C}=1\)
<=> \(\left(\sqrt{3}\cos\widehat{C}-1\right)^2+\cos^2\widehat{C}=1\)
<=> \(4\cos^2\widehat{C}-2\sqrt{3}\cos\widehat{C}=0\)( \(0^o< \widehat{C}< 90^o\))
<=> \(2\cos\widehat{C}-\sqrt{3}=0\)
<=> \(\cos\widehat{C}=\frac{\sqrt{3}}{2}\)
<=> \(\widehat{C}=30^o\)=> \(\widehat{B}=60^o\)
em cảm ơn cô nhiều lắm ạ <3