K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PH
1
15 tháng 6 2023
a: s=v*t
b: Theo đề, ta có: x/10-x/12=1/4
=>x/60=1/4
=>x=15
19 tháng 8 2021
a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
19 tháng 8 2021
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27
12 tháng 11 2021
\(x^2+y^2-2x+4y+8=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3\ge3\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Vậy GTNN là 3 khi x=1 và y=-2
=>Chọn B
TL
5
14 tháng 10 2018
1) \(x^2-5x-6=x^2-6x+x-6\)
\(=\left(x^2-6x\right)+\left(x-6\right)\)
\(=x\left(x-6\right)+\left(x-6\right)\)
\(=\left(x-6\right)\left(x+1\right)\)
2) \(2x^2-4xy+2y^2=2x^2-2xy-2xy+2y^2\)
\(=\left(2x^2-2xy\right)-\left(2xy-2y^2\right)\)
\(=2x\left(x-y\right)-2y\left(x-y\right)\)
\(=\left(x-y\right)\left(2x-2y\right)\)
\(=\left(x-y\right).2\left(x-y\right)\)
\(=2\left(x-y\right)^2\)
HỌC TỐT NHA !!
14 tháng 10 2018
\(x^2-6x+x-6\)
\(\left(x^2-6x\right)+\left(x-6\right)\)
\(x\left(x-6\right)+\left(x-6\right)\)
\(\left(x-6\right)\left(x+1\right)\)
\(x-6=0\) hoặc \(x+1=0\)
\(x=6\) hoặc \(x=-1\)
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
4 tháng 1 2022
a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
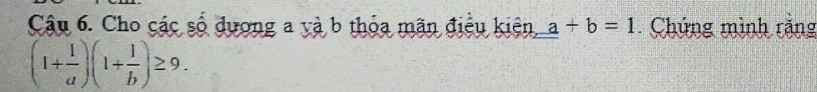
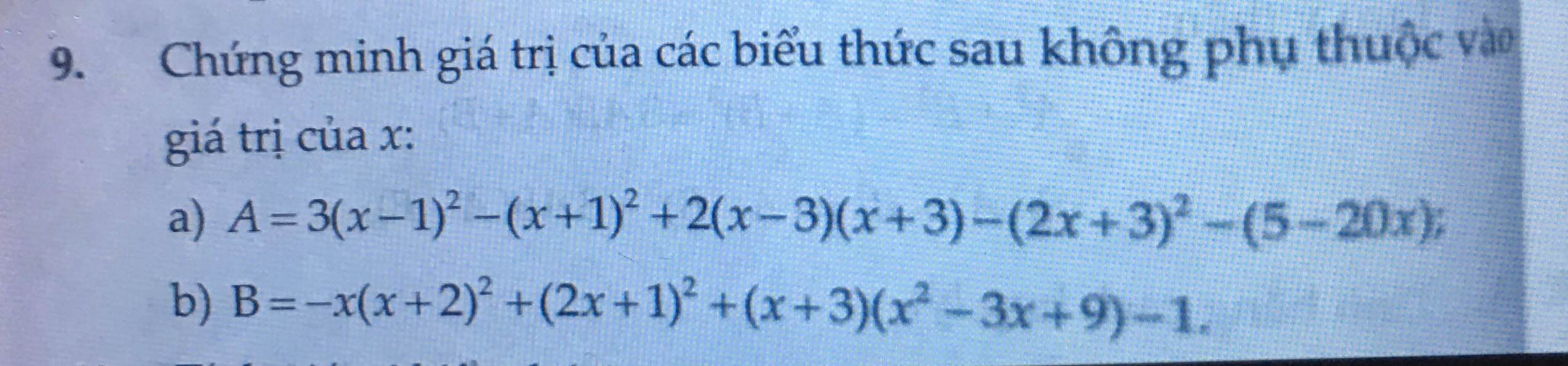
Đặt \(P=\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\)
\(P=1+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{ab}=1+\dfrac{a+b}{ab}+\dfrac{1}{ab}=1+\dfrac{2}{ab}\)
Với mọi a;b dương, ta có:
\(\left(a-b\right)^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+2ab+b^2\ge4ab\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Rightarrow4ab\le1\Rightarrow ab\le\dfrac{1}{4}\Rightarrow\dfrac{1}{ab}\ge4\)
\(\Rightarrow P\ge1+2.4=9\) (đpcm)
Dấu "=" xảy ra khi \(a=b=\dfrac{1}{2}\)