K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 10 2021
Bài 1:
a: \(2xy+3z+6y+xz\)
\(=2y\left(x+3\right)+z\left(x+3\right)\)
\(=\left(x+3\right)\left(z+2y\right)\)
b: \(x^2-6x-7\)
\(=x^2-7x+x-7\)
\(=\left(x-7\right)\left(x+1\right)\)
c: \(16x^2-\left(x+1\right)^2\)
\(=\left(4x-x-1\right)\left(4x+x+1\right)\)
\(=\left(3x-1\right)\left(5x+1\right)\)
7 tháng 10 2021
Bài 1:
a: \(2xy+3z+6y+xz\)
\(=2y\left(x+3\right)+z\left(x+3\right)\)
\(=\left(x+3\right)\left(z+2y\right)\)
b: \(x^2-6x-7\)
\(=x^2-7x+x-7\)
\(=\left(x-7\right)\left(x+1\right)\)
c: \(16x^2-\left(x+1\right)^2\)
\(=\left(4x-x-1\right)\left(4x+x+1\right)\)
\(=\left(3x-1\right)\left(5x+1\right)\)
6 tháng 7 2016
Xét △DEC và △BAC có
góc D chung
góc CDE= góc CBA (=90)
Vậy △DEC đồng dạng △BAC (g_g)
=> \(\frac{CD}{BC}=\frac{EC}{CA}\Rightarrow\frac{CD}{EC}=\frac{BC}{CA}\)
Xét △EAC và △DBC có
góc C chung
\(\frac{CD}{EC}=\frac{BC}{CA}\)(cmt)
Vậy △EAC đồng dạng △BDC (c_g_c)
=> góc CEA = góc CDB
Ta chứng minh được tam giác DHB vuông cân (góc H = 90 ,DH=HB)
=>gócHDB=45 hay là là góc BDA =45 (nó cùng là 1 góc nhưng do cách gọi tên thôi)
Ta có
\(\hept{\begin{cases}gocCEA+gocAEB=180^o\\gocCDB+gocBDA=180^0\end{cases}}\)
Mà góc CEA = góc CDB
=> góc AEB=góc BDA
Mà góc BDA=45
=> góc AEB=45
Xét tam giác EBA có
góc E=90
góc EBA=45
=>góc DAB =45
=> tam giác ABE vuông cân tại E
=> BA=BE
T I C K nha
____________________Chúc bạn học tốt ______________________
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
13 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
VD
1
VD
5
VD
3
31 tháng 5 2023
kết quả là : x2 - 3x + 1
số dư là : -1
bn tự đặt tính ra giúp mk nha, mk đang giải trên laptop nên ko chụp đc.
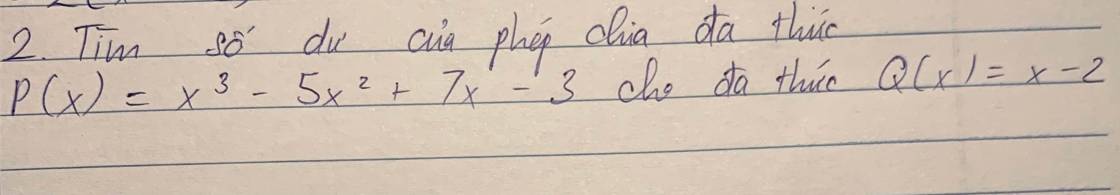
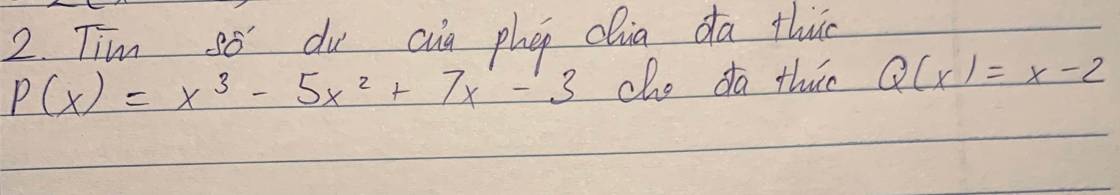
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AC^2=CH\cdot CB\)