
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1D nha bạn
Đây là mệnh đề chứa biến chứ không phải mệnh đề.

\(c,\) Để PT có 2 nghiệm \(x_1;x_2\Leftrightarrow\Delta=\left(m-4\right)^2+8\left(m-2\right)\ge0\)
\(\Leftrightarrow m^2-8m+16+8m-16\ge0\\ \Leftrightarrow m^2\ge0\left(\text{luôn đúng}\right)\)
Do đó PT có 2 nghiệm với mọi m
\(\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=\dfrac{m-4}{m-2}\left(1\right)\\x_1x_2=\dfrac{2}{2-m}\left(2\right)\end{matrix}\right.\)
Kết hợp \(x_1-x_2=3\text{ với }\left(1\right)\text{ ta được}\)
\(\left\{{}\begin{matrix}x_1=\left(\dfrac{m-4}{m-2}+3\right):2=\dfrac{4m-10}{m-2}\cdot\dfrac{1}{2}=\dfrac{2m-5}{m-2}\\x_2=\dfrac{m-4}{m-2}-\dfrac{2m-5}{m-2}=\dfrac{1-m}{m-2}\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2m-5\right)\left(1-m\right)}{\left(2-m\right)^2}=\dfrac{2}{2-m}\)
\(\Leftrightarrow\left(2m-5\right)\left(1-m\right)=2\left(2-m\right)\\ \Leftrightarrow7m-2m^2-5=4-2m\\ \Leftrightarrow2m^2-9m+9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m=3\text{ và }m=\dfrac{3}{2}\) thỏa đề bài

d. \(\dfrac{\pi}{2}< a;b< \pi\Rightarrow sina>0;sinb>0\)
\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{4}{3}\)
\(sinb=\sqrt{1-cos^2b}=\dfrac{5}{13}\Rightarrow tanb=-\dfrac{5}{12}\)
Vậy:
\(sin\left(a-b\right)=sina.cosb-cosa.sinb=\dfrac{4}{5}.\left(-\dfrac{12}{13}\right)-\left(-\dfrac{3}{5}\right)\left(\dfrac{5}{13}\right)=...\)
\(cos\left(a-b\right)=cosa.cosb-sina.sinb=...\) (bạn tự thay số bấm máy)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=...\)
\(cot\left(a+b\right)=\dfrac{1}{tan\left(a+b\right)}=\dfrac{1-tana.tanb}{tana+tanb}=...\)
e.
\(0< y< \dfrac{\pi}{2}\Rightarrow cosy>0\Rightarrow cosy=\sqrt{1-sin^2y}=\dfrac{4}{5}\)
\(\Rightarrow tany=\dfrac{siny}{cosy}=\dfrac{3}{4}\)
Vậy: \(tan\left(x+y\right)=\dfrac{tanx+tany}{1-tanx.tany}=...\)
\(cot\left(x-y\right)=\dfrac{1}{tan\left(x-y\right)}=\dfrac{1+tanx.tany}{tanx-tany}=...\)


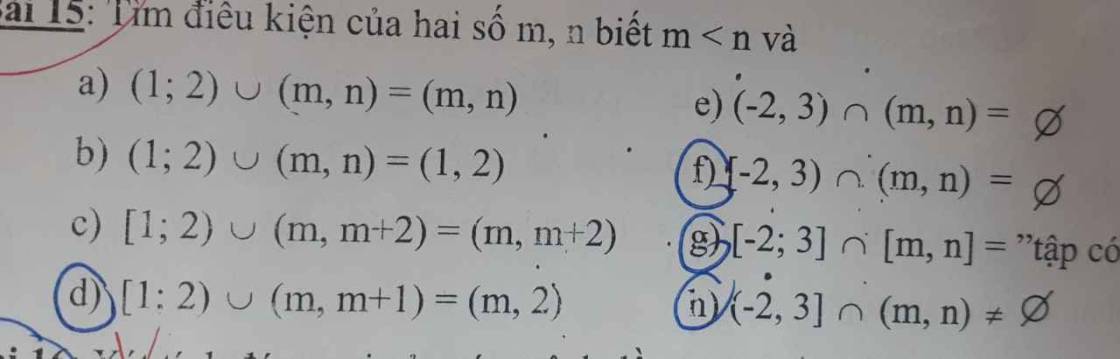




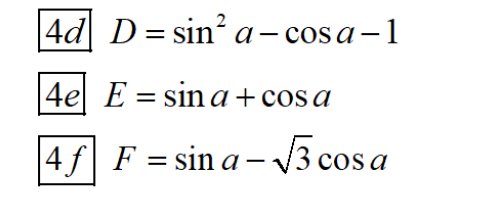
 Cứu tớ câu khoanh tròn í
Cứu tớ câu khoanh tròn í



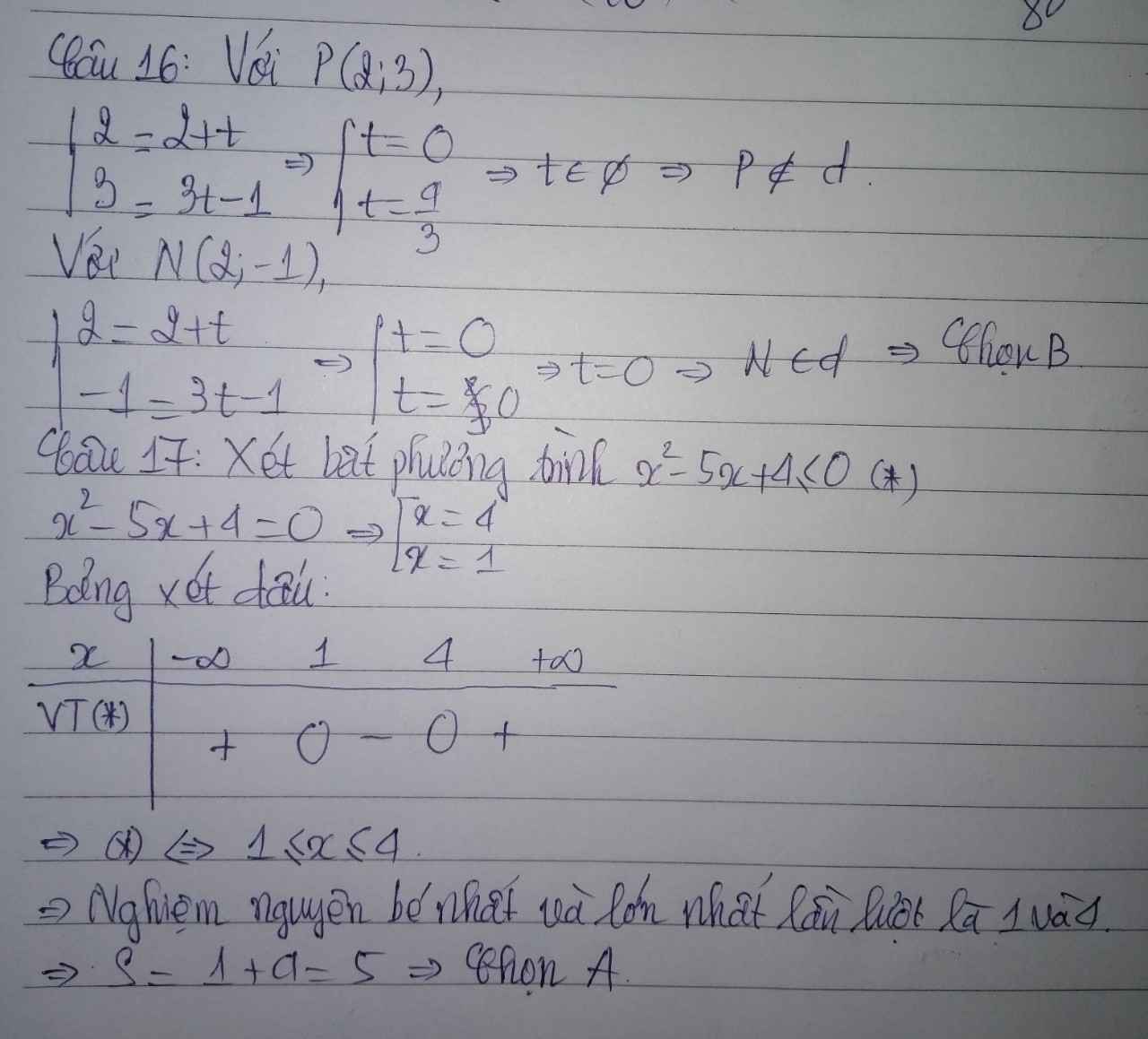
 giúp mình mấy câu này với mình cảm ơn nhìu ạ
giúp mình mấy câu này với mình cảm ơn nhìu ạ
f: [2;3) giao (m;n)=rỗng
=>m>=3 hoặc n<2
n: (-2;3] giao (m,n) khác rỗng
=>m<=3 và n>=-2