
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(c,\) Để PT có 2 nghiệm \(x_1;x_2\Leftrightarrow\Delta=\left(m-4\right)^2+8\left(m-2\right)\ge0\)
\(\Leftrightarrow m^2-8m+16+8m-16\ge0\\ \Leftrightarrow m^2\ge0\left(\text{luôn đúng}\right)\)
Do đó PT có 2 nghiệm với mọi m
\(\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=\dfrac{m-4}{m-2}\left(1\right)\\x_1x_2=\dfrac{2}{2-m}\left(2\right)\end{matrix}\right.\)
Kết hợp \(x_1-x_2=3\text{ với }\left(1\right)\text{ ta được}\)
\(\left\{{}\begin{matrix}x_1=\left(\dfrac{m-4}{m-2}+3\right):2=\dfrac{4m-10}{m-2}\cdot\dfrac{1}{2}=\dfrac{2m-5}{m-2}\\x_2=\dfrac{m-4}{m-2}-\dfrac{2m-5}{m-2}=\dfrac{1-m}{m-2}\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2m-5\right)\left(1-m\right)}{\left(2-m\right)^2}=\dfrac{2}{2-m}\)
\(\Leftrightarrow\left(2m-5\right)\left(1-m\right)=2\left(2-m\right)\\ \Leftrightarrow7m-2m^2-5=4-2m\\ \Leftrightarrow2m^2-9m+9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m=3\text{ và }m=\dfrac{3}{2}\) thỏa đề bài

f: [2;3) giao (m;n)=rỗng
=>m>=3 hoặc n<2
n: (-2;3] giao (m,n) khác rỗng
=>m<=3 và n>=-2

Ta có B=\(\frac{2009^{2010}-2}{2009^{2011}-2}\)<1
=>\(\frac{2009^{2010}-2}{2009^{2011}-2}\)<\(\frac{2009^{2010}-2+3}{2009^{2011}-2+3}\)=\(\frac{2009^{2010}+1}{2009^{2011}+1}\)(1)
Mà \(\frac{2009^{2010}+1}{2009^{2011}+1}\)<1
=> \(\frac{2009^{2010}+1}{2009^{2011}+1}\)<\(\frac{2009^{2010}+1+2008}{2009^{2011}+1+2008}\)=\(\frac{2009^{2010}+2009}{2009^{2011}+2009}\)=\(\frac{2009\cdot\left(2009^{2009}+1\right)}{2009\cdot\left(2009^{2010}+1\right)}\)=\(\frac{2009^{2009}+1}{2009^{2010}+1}\)=A(2)
Từ (1)và(2)=>B<\(\frac{2009^{2010}+1}{2009^{2011}+1}\)<A=>B<A hay A>B

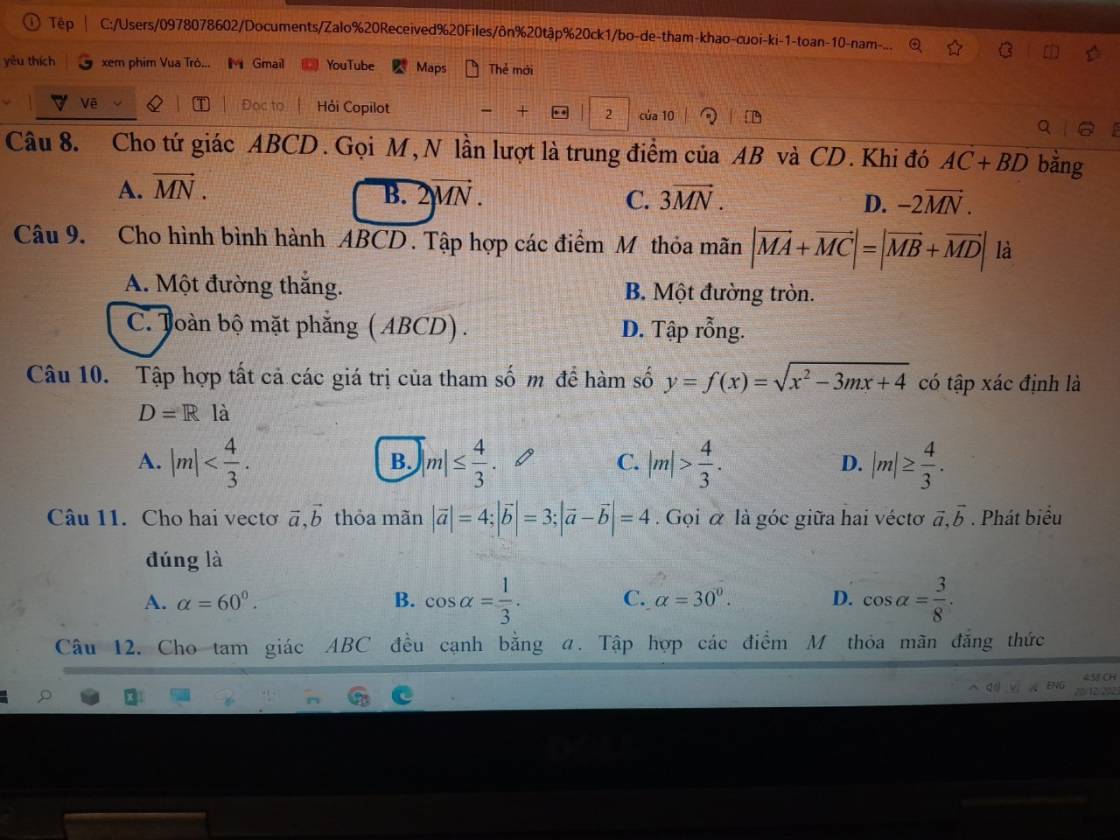
Câu 9:
Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>O là trung điểm chung của AC và BD
Vì O là trung điểm của AC
nên \(\overrightarrow{MA}+\overrightarrow{MC}=2\cdot\overrightarrow{MO}\)
Vì O là trung điểm của BD
nên \(\overrightarrow{MB}+\overrightarrow{MD}=2\cdot\overrightarrow{MO}\)
=>\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\)
=>Chọn C


 Cứu tớ câu khoanh tròn í
Cứu tớ câu khoanh tròn í
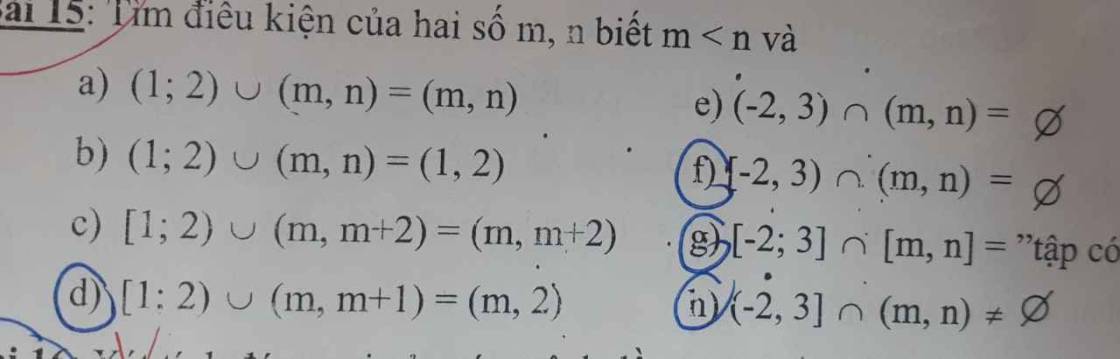

 giúp tớ câu 9 với ạ
giúp tớ câu 9 với ạ nhanh nhé tớ trước 7:45 rồi
nhanh nhé tớ trước 7:45 rồi giúp tớ câu c nhá
giúp tớ câu c nhá
1D nha bạn
Đây là mệnh đề chứa biến chứ không phải mệnh đề.